ПримерЫ расчета рам методом перемещений
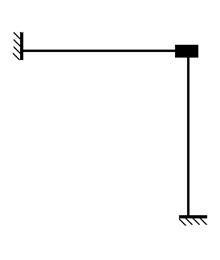
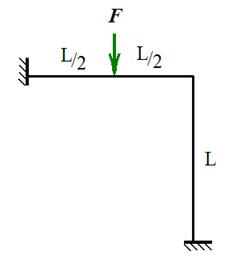
Пример 1. Рассчитаем раму, изображенную на рис. 33. Рама один раз кинематически неопределима. Образуем основную систему метода перемещений, устранив угол поворота узла (рис. 34).
Рис. 33 Рис. 34
Составляем каноническое уравнение (4). Для этого рассматриваем состояние основной системы под действием внешней силы (рис. 35), строим эпюру изгибающих моментов
Рис. 35 Рис. 36
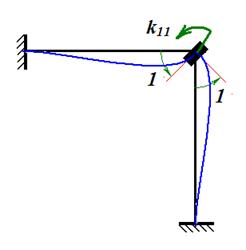
Далее рассматриваем состояние основной системы при «единичном» угле поворота узла (рис. 37), строим соответствующую эпюру моментов
Рис. 37 Рис. 38
Полный реактивный момент в заделке равен нулю, поэтому
Находим угол поворота узла рамы
Вычисляем изгибающие моменты в заданной раме по правилу суперпозиции
Суммарная эпюра изгибающих моментов представлена на рис. 39.
Проверка расчета осуществляется так же, как в методе сил, вычислением перемещения закрепленного сечения с помощью интеграла Мора. Пример 2. Рассчитаем раму, изображенную на рис. 40.
Рис. 40
На рис. 41 показан примерный вид деформированной рамы. По условиям симметрии системы углы поворота и вертикальные перемещения в узлах A, B, C, D одинаковы. Введем групповые перемещения
Рис. 41
Рис. 42
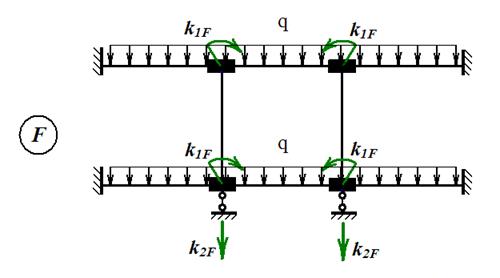
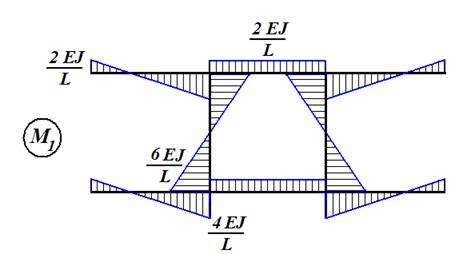
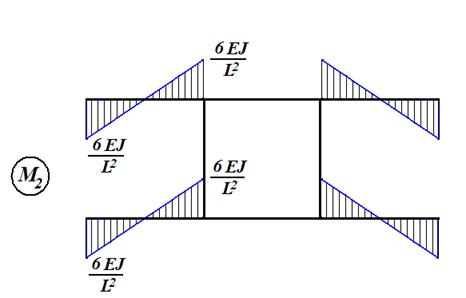
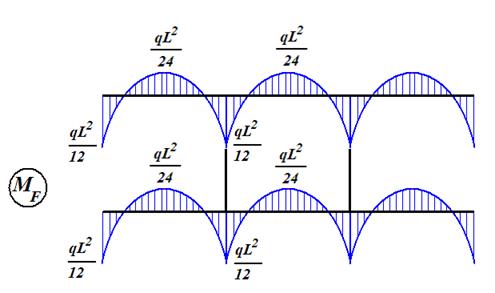
Для составления канонических уравнений (5) последовательно рассматриваем три состояния основной системы: · состояние 1 (рис. 43), возникающее при одновременном повороте «плавающих» заделок в узлах A, B, C, D на «единичные» углы; · состояние 2 (рис. 44), возникающее при одновременном вертикальном смещении узлов на единицу; · состояние F (рис. 45), возникающее при действии заданных внешних сил и закрепленных узлах.
Рис. 43
Рис. 44
Рис. 45
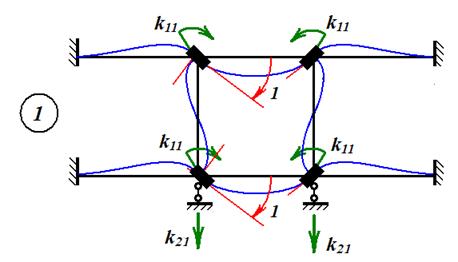
На рис. 46, 47, 48 показаны распределения изгибающих моментов в стержнях рамы в каждом из указанных состояний.
Рис. 46
Рис. 47
Рис. 48
Зная распределение изгибающих моментов, находим реакции дополнительных связей из условий равновесия узлов: · в состоянии 1 · в состоянии 2 · в состоянии F Таким образом, уравнения метода перемещений составлены. Их решение имеет вид
Заметим, что кажущаяся асимметрия матрицы жесткости ( После определения перемещений узлов, применяя принцип суперпозиции, вычисляем изгибающие моменты в заданной раме
Полученная эпюра моментов показана на рис. 49.
Рис. 49
|

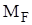 (рис. 36) и находим реакцию дополнительной связи
(рис. 36) и находим реакцию дополнительной связи 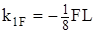 .
.

 (рис.38) и находим момент в дополнительной заделке
(рис.38) и находим момент в дополнительной заделке 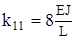 .
.

 .
. .
. .
.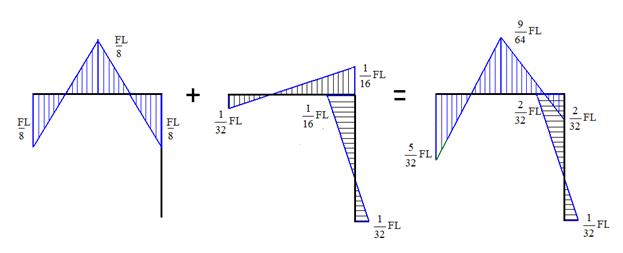 Рис. 39
Рис. 39
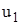 ,
, 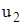 , т.е. перемещения, единые для группы узлов. Степень кинематической неопределимости рамы равна двум. Запретив указанные перемещения с помощью дополнительных связей, образуем основную систему метода перемещений (рис. 42).
, т.е. перемещения, единые для группы узлов. Степень кинематической неопределимости рамы равна двум. Запретив указанные перемещения с помощью дополнительных связей, образуем основную систему метода перемещений (рис. 42).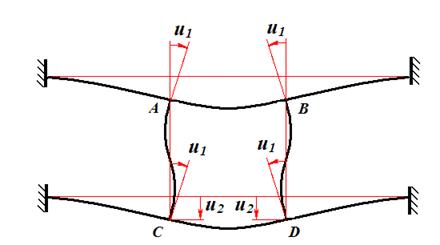


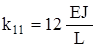 ,
, 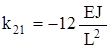 ;
;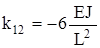 ,
, 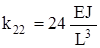 ;
;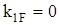 ,
, 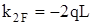 .
.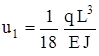 ,
, 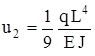 .
.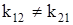 ) в этом примере связана с введением групповых перемещений. Реакции второй дополнительной связи оказываются удвоенными. Симметрия легко восстанавливается умножением всех членов второго уравнения на коэффициент ½.
) в этом примере связана с введением групповых перемещений. Реакции второй дополнительной связи оказываются удвоенными. Симметрия легко восстанавливается умножением всех членов второго уравнения на коэффициент ½.
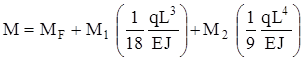 .
.



