Заключительное замечание
Идея расчета конструкций с использованием перемещений узлов в качестве основных искомых величин получила развитие в наиболее мощном современном методе анализа напряженного состояния конструкций – методе конечных элементов (МКЭ). При расчете МКЭ конструкцию представляют как совокупность конечных (типовых) элементов, связанных между собой в узлах. Специалистами разработаны многочисленные типы конечных элементов, предназначенных для расчета конструкций по стержневым, оболочечным, трехмерным и комбинированным моделям. Важно, что для любого конечного элемента методами теории упругости устанавливается связь между перемещениями узлов
здесь Соотношение (21) аналогично по смыслу соотношению (12) для типового элемента рамы. К сожалению, решить уравнения (21) относительно перемещений Из множества конечных элементов собирается расчетная модель конструкции, для которой уравнения МКЭ имеют вид, схожий с уравнениями (21):
однако здесь Очевидно, что при сборке конечных элементов неизвестные внутренние силы взаимодействия между элементами взаимно уничтожаются, т.е. исчезают из уравнений. Система уравнений становится замкнутой. Заметим, что канонические уравнения метода перемещений (6) приобретают вид (22), характерный для МКЭ, если вместо вектора реакций
ЛИТЕРАТУРА 1. Благонадежин В.Л., Окопный Ю.А., Чирков В.П. Механика материалов и конструкций. – М.: Издательство МЭИ, 1994. – 312 с. 2. Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика. Стержневые системы. – М.: Стройиздат, 1981. – 512 с. 3. Спицына Д.Н. Строительная механика стержневых машиностроительных конструкций. - М.: Высшая школа, 1977. - 248 с. 4. Усюкин В.И. Строительная механика конструкций космической техники. – М.: Машиностроение, 1988. – 390 с.
|

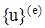 и действующими в узлах силами
и действующими в узлах силами 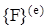 :
: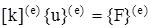 , (21)
, (21)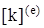 - матрица жесткости конечного элемента, верхний индекс указывает на отношение величины к отдельному конечному элементу.
- матрица жесткости конечного элемента, верхний индекс указывает на отношение величины к отдельному конечному элементу. , (22)
, (22)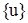 - вектор перемещений всех узлов конструкции, т.е. ансамбля конечных элементов;
- вектор перемещений всех узлов конструкции, т.е. ансамбля конечных элементов; 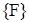 - вектор внешних нагрузок, приведенных к узлам конструкции;
- вектор внешних нагрузок, приведенных к узлам конструкции; 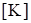 - матрица жесткости конструкции.
- матрица жесткости конструкции.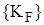 ввести противоположный вектор
ввести противоположный вектор 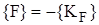 , компоненты которого следует трактовать как внешние узловые силы, т.е. силы, приведенные к узлам рамы.
, компоненты которого следует трактовать как внешние узловые силы, т.е. силы, приведенные к узлам рамы.


