Реакции связей от заданных внешних сил
Определим реакции в заделках для балки, нагруженной в произвольном сечении сосредоточенной силой (рис. 27). Эта задача является весьма важной, т.к. зная ее решение и используя принцип суперпозиции, можно получить результат для произвольной нагрузки. Поставленную задачу можно решить традиционными методами, например, методом сил или с помощью интегрирования дифференциального уравнения изогнутой оси балки. Мы воспользуемся методом, основанным на принципе взаимности работ. Состояние балки при действии внешней силы будем называть первым. Реакции определяются поочередно. Для определения реакции
Согласно принципу взаимности работ, работа Из пяти сил, действующих в первом состоянии (см. рис. 27), совершают работу лишь две силы – искомая Имеем
где Силы второго состояния не совершают работу на перемещениях первого состояния, поэтому Из уравнения принципа взаимности работ
следует
Полученный результат позволяет сформулировать общее правило определения реакций. Для определения реакции связи необходимо вычислить работу заданной внешней нагрузки на перемещениях, связанных с «единичным» смещением в направлении искомой реакции, и взять работу со знаком минус. Прогибы балки во втором состоянии уже изучались. Была получена функция (7). Таким образом, прогиб под силой во втором состоянии
искомая реакция
Аналогично выражаются остальные реакции, причем в качестве прогибов второго состояния последовательно рассматриваются полиномы Эрмита (8) - (10). В результате
Приведем значения реакций
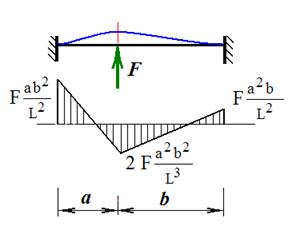
На рис. 29 показана эпюра изгибающих моментов в балке. Если сила
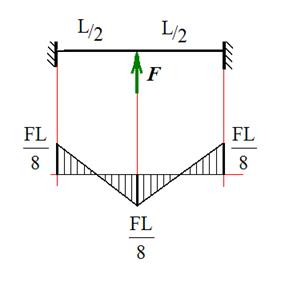
Для этого частного случая эпюра изгибающих моментов показана на рис. 30.
Рис. 29 Рис. 30
Рассмотрим определение реакций в заделках при произвольной распределенной нагрузке
Рис. 31
Применяя изложенную процедуру принципа взаимности работ, считаем работу распределенной нагрузки на прогибах балки при втором (виртуальном) состоянии, в качестве которого последовательно выбирается одно из четырех изученных видов деформации балки:
где Найдем реакции при действии равномерно распределенной нагрузки, т.е. при В этом случае интегралы (19) принимают вид
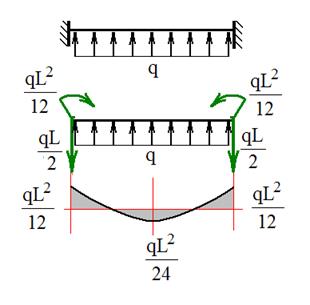
Вычисляя интегралы, получаем значения реакций
На рис. 32 показаны реакции в действительных направлениях и эпюра изгибающих моментов.
Подведем итог. Получены жесткости типового элемента плоских рам и реакции в заделках элемента при действии внешних сил. Эти результаты позволяют составлять уравнения метода перемещений (6) для расчета рам. После определения узловых перемещений, как правило, требуется построить эпюры изгибающих моментов в раме. Решая вспомогательные задачи, мы установили распределение изгибающих моментов в типовом элементе при различных видах его деформации и нагружения (см. эпюры на рис. 17, 20, 29, 30, 32). Вспомним, что для формирования уравнений метода перемещений (6) рассматривались состояния основной системы при действии внешних сил и при «единичных» перемещениях узлов. Эпюры моментов для каждого из этих состояний могут быть построены с привлечением найденных решений вспомогательных задач. Обозначим функцию моментов в основной системе от заданных внешних сил через Моменты в рассчитываемой раме определяются путем суперпозиции
где
|

 выберем в качестве второго состояния форму деформации балки при «единичном» перемещении по направлению искомой реакции, т.е. по направлению 1 (рис. 28).
выберем в качестве второго состояния форму деформации балки при «единичном» перемещении по направлению искомой реакции, т.е. по направлению 1 (рис. 28).
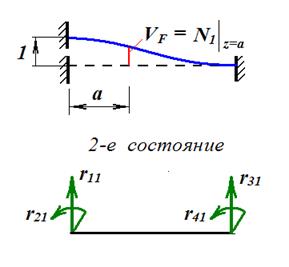 Рис. 27 Рис. 28
Рис. 27 Рис. 28 сил первого состояния на соответствующих им перемещениях второго состояния равна работе
сил первого состояния на соответствующих им перемещениях второго состояния равна работе 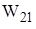 сил второго состояния на соответствующих им перемещениях первого состояния. Итак,
сил второго состояния на соответствующих им перемещениях первого состояния. Итак, 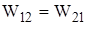 .
.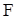 .
. ,
,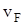 - перемещение в точке приложения силы
- перемещение в точке приложения силы 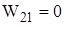 .
. ,
, . (13)
. (13) ,
,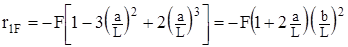 . (14)
. (14)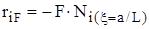
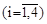 . (15)
. (15)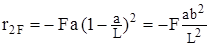 , (16)
, (16) , (17)
, (17)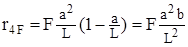 . (18)
. (18) приложена посредине балки, то при
приложена посредине балки, то при 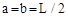 формулы (14), (16) - (18) дают
формулы (14), (16) - (18) дают ,
, 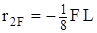 ,
,  .
.
 (рис. 31).
(рис. 31).
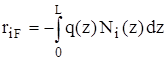 ,
, 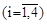 (19)
(19) - полиномы Эрмита (7) – (10), согласно сформулированному правилу определения реакций работа берется со знаком минус.
- полиномы Эрмита (7) – (10), согласно сформулированному правилу определения реакций работа берется со знаком минус.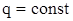 .
.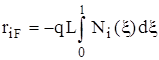 .
.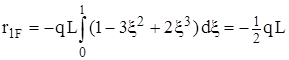 , (очевидный результат)
, (очевидный результат)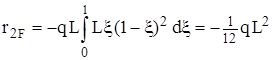 ,
,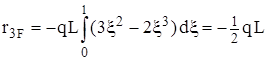 , (также очевидный результат)
, (также очевидный результат)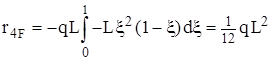 .
.
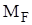 , функции моментов в основной системе при «единичных» перемещениях узлов через
, функции моментов в основной системе при «единичных» перемещениях узлов через 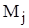 , где индекс
, где индекс 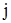 указывает номер (направление) узлового перемещения.
указывает номер (направление) узлового перемещения. , (20)
, (20) - вычисленные узловые перемещения,
- вычисленные узловые перемещения,  - общее число введенных узловых перемещений (степень кинематической неопределимости конструкции).
- общее число введенных узловых перемещений (степень кинематической неопределимости конструкции).


