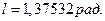Единицы измерения углов и дуг
В теоретических зависимостях углы и дуги обычно выражают в радианах. За единицу радианной меры принят радиан - центральный угол, стягиваемый дугой, длина которой равна радиусу окружности. Произвольный угол
Радиус Градусная мера углов и дуг применяется в практических задачах. Если в радианной мере углы и дуги выражаются в долях радиуса окружности, то в градусной они измеряются в долях самой окружности. За единицу вградусной мере принят градус - Часто при вычислениях приходится переходить от радианной меры к градусной и наоборот. Основным переводным множителем для таких переходов служит
Заданный в градусах угол переводится в радианную меру на основе равенства:
Для перехода от радианной меры к градусной пользуются соотношением
Если угол или дуга заданы в минутах дуги, то переводным множителем служит
Следовательно,
Задача 1. Выразить в радианах углы Решение.
Задача 2. Выразить в градусной мере дугу
|
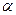(рад) выражается отношением дуги 
, на которую он опирается, к радиусу 
этой дуги: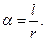
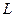содержит 
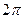радиан.
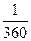часть окружности. Градус 
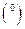делится на более мелкие (дольные) единицы - минуты 
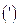и секунды дуги 
.
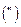- величина дуги, соответствующая центральному углу, равному 
:
:
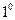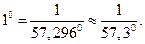
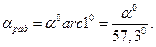
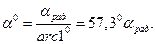
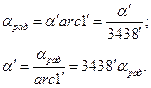
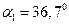и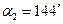 
.
