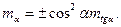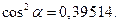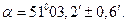Задачи для самостоятельного решения. Задача 26. В методе «траверзного расстояния» (частный случай крюйс-пеленга) расстояние до предмета по второму пеленгу определяется по формуле:
Задача 26. В методе «траверзного расстояния» (частный случай крюйс-пеленга) расстояние до предмета по второму пеленгу определяется по формуле: Рассчитать расстояние Задача 27. Дальность видимости огня в море рассчитана по формуле: Рассчитать дальность видимости огня и ее СКП (СКО), если высота предмета Задача 28. Скорость течения может быть вычислена по скорости истинного ветра:
Рассчитать скорость ветрового течения и СКП (СКО) Задача 29. При больших углах дрейфа истинное расстояние
где
Рассчитать Задача 30. Необходимый для работы трос можно подобрать, рассчитав его разрывную крепость
где Р - допускаемый расчетный предел прочности троса, кгс/см2;
Вычислить Задача 31. Стрелка провиса буксирного троса
где
Рассчитать Задача 32. Площадь равнобедренного треугольника вычисляется по формуле:
где
Рассчитать Задача 33. Площадь параллелограмма вычисляется по формуле:
где
Рассчитать
Задача 34. При приведении высоты светила к одному моменту вычисляют величину
где
Рассчитать СКП (СКО)
II. Общую формулу СКП (СКО)
или
Когда известна погрешность (ошибка)
Задача 35. Секстаном измерен угол Решение. 1. Продифференцируем функцию
и переходим к погрешностям (ошибкам):
2. Подставим числовые значения
3. Выполним расчеты:
Находим Задача 36. Задан Найти аргумент Решение. 1. Чтобы составить расчетную формулу для вычисления
2. Переходим к средним квадратическим погрешностям (ошибкам):
откуда
3. По величине 4. Затем находим: После чего подставили числовые величины в формулу:
5. Выразим погрешность (ошибку)
Следовательно,
|


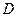 и СКП (СКО) расстояния
и СКП (СКО) расстояния  , если плавание
, если плавание  мили и курсовой угол
мили и курсовой угол 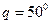 ,
,  кб;
кб; 
 .
.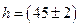 м, а высота глаза
м, а высота глаза 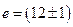 м.
м.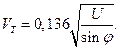
 , если скорость истинного ветра
, если скорость истинного ветра  м/c;
м/c;  м/с; широта места судна
м/с; широта места судна 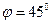 ;
; 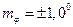 .
.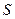 , проходимое судном, определяется по формуле:
, проходимое судном, определяется по формуле:
 - расстояние, пройденное судном по лагу, мили;
- расстояние, пройденное судном по лагу, мили; - угол дрейфа,
- угол дрейфа,  .
. , если
, если 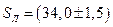 мили;
мили; 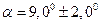 .
. (кгс) по формуле:
(кгс) по формуле:
 - диаметр троса, см.
- диаметр троса, см. , если
, если  кгс;
кгс;  см.
см. (м) рассчитывается по формуле:
(м) рассчитывается по формуле:
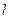 - длина буксирного троса, м;
- длина буксирного троса, м;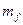 по следующим данным;
по следующим данным;  м;
м;  .
.
 - длина одной из равных сторон;
- длина одной из равных сторон; если
если  м;
м; 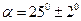 .
.
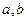 - стороны параллелограмма;
- стороны параллелограмма; м;
м;  м;
м;  см;
см;  ;
; 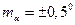 .
.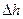 по формуле:
по формуле: ,
, - широта места судна;
- широта места судна; - азимут светила;
- азимут светила; - момент времени, за который производится приведение высоты.
- момент времени, за который производится приведение высоты.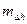 , если
, если  ;
;  . Величина
. Величина  мин 22 с.
мин 22 с. можно применить для вычисления погрешности (ошибки) тригонометрической функции, когда известна погрешность (ошибка)
можно применить для вычисления погрешности (ошибки) тригонометрической функции, когда известна погрешность (ошибка) 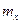 измерения или задания аргумента - угла или дуги:
измерения или задания аргумента - угла или дуги:


 с погрешностью (ошибкой)
с погрешностью (ошибкой)  Найти
Найти  и СКП (СКО)
и СКП (СКО)  .
.
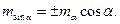
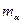 . и
. и 
 ед. 5-го разряда.
ед. 5-го разряда. 
 .
. с погрешностью (ошибкой)
с погрешностью (ошибкой)  .
.