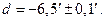Вероятнейшего значения измеряемой величины
1. Если истинные случайные погрешности (ошибки) серии наблюдений подчиняются нормальному закону, СКП (СКО)
Здесь символ Величины случайных погрешностей (ошибок)
где Задача 3. На береговой радиолокационной станции взяли 6 отсчетов расстояния до точечного ориентира. Расстояние, снятое с плана, приняли за истинное Решение (см. таблицу). 1. Вычислим истинные случайные погрешности (ошибки)
2. Рассчитаем сумму квадратов случайных погрешностей (ошибок). 3. Вычислим СКП (СКО)
Округлив результат, получим
Задача 4. Из наблюдений получили группу значений полудиаметра Солнца. Величину полудиаметра, указанную на данный месяц в Морском астрономическом ежегоднике, приняли за истинное значение. Требуется вычислить СКП (СКО) одного наблюдения. Решение (см. таблицу).
СКП (СКО) одного наблюдения
II. Формула (1) применима только в расчетах теоретического характера, так как истинные значения измеряемых величин, а, следовательно, и истинные случайные погрешности (ошибки) наблюдений никогда не бывают известны. В практических задачах оценку точности производят, пользуясь формулой Бесселя:
В формуле (3) через
Одновременно со СКП (СКО)
Вычисления следует производить в таком порядке: 1) по результатам
2) вычислить вероятнейшие погрешности (ошибки) 3) найти СКП (СКО) 4) вычислить СКП (СКО) Задача 5. Следуя малым ходом, несколько раз подряд определили по РЛС расстояние до мыса, находящегося вблизи траверза, и получили следующие отсчеты:
Найти вероятнейшее значение расстояния до мыса, СКП (СКО) Решение. 1. Вычислим вероятнейшее значение расстояния:
2. В табличной форме рассчитаем вероятнейшие погрешности (ошибки)
Отличие суммы уклонений от нуля 3. Вычислим СКП (СКО)
Таким образом, измеренное радиолокатором расстояние до мыса Задача 6. С помощью наклономера выполнили серию наблюдений наклонения видимого горизонта:
Вычислить вероятнейшее значение наклонения и произвести оценку точности наблюдений и измерения. Решение (см. таблицу), 1. По результатам наблюдении вычислим вероятнейшее значение наклонения:
2. Рассчитаем сумму квадратов уклонений
3. Вычислим СКП (СКО)
Итак,
|

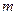 одного наблюдения вычисляют по формуле:
одного наблюдения вычисляют по формуле: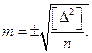 (1)
(1) обозначает сумму квадратов истинных случайных погрешностей (ошибок), а буквой
обозначает сумму квадратов истинных случайных погрешностей (ошибок), а буквой 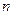 обозначено число наблюдений в серии.
обозначено число наблюдений в серии. результатов
результатов  наблюдений предварительно вычисляются по формуле:
наблюдений предварительно вычисляются по формуле: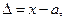 (2)
(2) - истинное значение измеряемой величины.
- истинное значение измеряемой величины.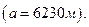 Вычислить СКП (СКО)
Вычислить СКП (СКО)  наблюдений по формуле (2).
наблюдений по формуле (2).
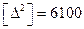
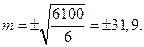
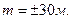


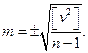 (3)
(3)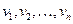 обозначены вероятнейшие случайные погрешности (ошибки) результатов наблюдений, или, иначе, уклонения результатов наблюдений от вероятнейшего значения
обозначены вероятнейшие случайные погрешности (ошибки) результатов наблюдений, или, иначе, уклонения результатов наблюдений от вероятнейшего значения 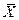
 измеряемой величины:
измеряемой величины: (4)
(4)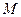 вероятнейшего значения измеряемой величины по формуле:
вероятнейшего значения измеряемой величины по формуле: (5)
(5)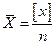


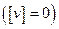 проверим правильность вычислений среднего арифметического
проверим правильность вычислений среднего арифметического  и уклонений от него.
и уклонений от него.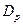 , кб.
, кб.
 , кб.
, кб.

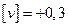
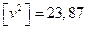

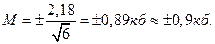
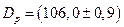 кб.
кб.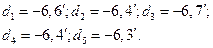

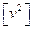 .
.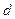 , мин. дуги
, мин. дуги
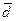 , мин. дуги
, мин. дуги
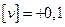
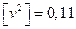
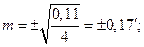
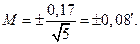

 и
и