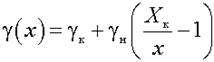Класс точности средств измерений
Это характеристика, определяющая гарантированные границы значений основных и дополнительных погрешностей, а также другие свойства средств измерений, влияющих на точность. Соответствие погрешности СИ приписанному им классу точности во время эксплуатации проверяется при периодических поверках. Если погрешность оказывается меньше нормированных значений, то СИ продолжает эксплуатироваться, если нет, то подлежит ремонту и регулировке. Основные способы установления пределов допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ 8.401-80. Основная погрешность СИ нормируется четырьмя различными способами. Чтобы четко уяснить себе эти различия и грамотно использовать нормируемые значения при расчёте погрешностей результатов измерения, необходимо рассмотреть характер изменения относительной и абсолютной погрешности СИ в диапазоне значений измеряемой величины и обусловленные этим положения стандартов, регламентирующих нормирование погрешностей средств измерений. Основное различие в способах нормирования обусловлено разным соотношением аддитивной и мультипликативной составляющих в погрешности тех или иных СИ.
При чисто мультипликативной полосе погрешностей СИ (см. рис. 1.2, б) абсолютная погрешность Δ(х) возрастает прямо пропорционально текущему значению х измеряемой величины. Поэтому относительная погрешность, т.е. погрешность чувствительности такого преобразователя,
Таким способом нормируются погрешности масштабных преобразователей (делителей напряжения, шунтов, измерительных трансформаторов тока и напряжения и т. п.). Их класс точности указывается в виде значения γ s, выраженного в процентах. Граница относительной погрешности результата измерения γ(х) в этом случае постоянна и при любом х просто равна значению γ s, а абсолютная погрешность результата измерения рассчитывается по формуле
Δ(х) = γ s x.
Если бы эти соотношения оставались справедливыми для всего диапазона возможных значений измеряемой величины х от 0 до X к (X к – предел диапазона измерений), то такие измерительные преобразователи были бы наиболее совершенными, так как они имели бы бесконечно широкий рабочий диапазон, т. е. обеспечивали бы с той же погрешностью измерение сколь угодно малых значений х. Однако реально таких преобразователей не существует, так как невозможно создать преобразователь, полностью лишённый аддитивных погрешностей. Эти погрешности от шума, дрейфа, трения, наводок, вибраций и т. п. неизбежны в любых типах СИ. Поэтому для реальных СИ, погрешность которых нормируется лишь одним числом – погрешностью чувствительности γ s, – всегда указываются границы рабочего диапазона, в которых такая оценка остаётся приближённо справедливой.
При чисто аддитивной полосе погрешностей (см. рис. 1.2, а) остаётся неизменной для любых значений х граница абсолютной погрешности нуля
Но нормировать абсолютное значение Δ o неудобно, так как для многопредельных приборов оно будет различным для каждого поддиапазона, и в паспорте прибора пришлось бы перечислять эти значения для всех поддиапазонов. Поэтому нормируют не абсолютное Δ o, а приведённое значение этой погрешности:
Стандарт 8.401-80 определяет для приборов с равномерной или степенной шкалой, если нулевая отметка находится на краю или вне шкалы, нормирующее значение Х N равным верхнему пределу диапазона измерений. Если же нулевая отметка находится посредине шкалы, то Х N равно протяжённости диапазона измерений (например, для амперметра со шкалой от -30 до +60 А значение
Значение приведённой погрешности γ o, выраженное в процентах, используется для обозначения класса точности таких СИ. Однако полагать, как уже указывалось, что вольтметр класса точности 1,0 обеспечивает во всём диапазоне измерений получение результатов с погрешностью ±1%, – грубейшая ошибка. В действительности текущее значение относительной погрешности
т. е. растёт обратно пропорционально х и изменяется по гиперболе (рис. 1.4). Таким образом, относительная погрешность γ(х) равна классу точности прибора γ o лишь на последней отметке шкалы (при х = Х к). При х = 0,1Х к она в 10 раз больше γ o, а при дальнейшем уменьшении х стремится к бесконечности. При уменьшении измеряемой величины х до значения абсолютной погрешности нуля Δ o относительная погрешность результата измерения достигает
Такое значение измеряемой величины, когда
Отсюда полный диапазон D п измеряемых величин для любого преобразователя ограничивается снизу порогом чувствительности, а сверху – пределом измерений. Так как в области малых значений х погрешность измерений очень велика, то рабочий диапазон D р ограничивают снизу таким значением х, где относительная погрешность измерений γ(х) не превосходит ещё некоторого заранее заданного значения γ з, равного, например, 4, 10 или 20%. Таким образом, рабочий диапазон назначается достаточно произвольно (см. рис. 1.4) и составляет только некоторую часть полного диапазона СИ. В начальной же части шкалы измерения недопустимы, в чём и заключается отрицательное влияние аддитивной погрешности, не позволяющее использовать один и тот же преобразователь для измерения как больших, так и малых измеряемых величин.
При одновременном присутствии аддитивной и мультипликативной составляющих полоса погрешностей имеет трапецеидальную форму (рис. 1.5, а), а текущее значение абсолютной погрешности Δ(х) в функции измеряемой величины х описывается соотношением
где Δ o – аддитивная, а γ s х – мультипликативная составляющие абсолютной погрешности.
Если все члены уравнения (1.1) разделить на предел измерений Х к, то для приведённого значения погрешности получим
Приведённое значение погрешности в начале диапазона (при х = 0) обозначим через Δ o / Х к = γ н. Тогда соотношение (1.2) примет вид
и изобразится графиком рис. 1.5, б. Таким образом, при наличии у СИ и аддитивной, и мультипликативной составляющих погрешности его приведённая погрешность линейно возрастает от
т. е. при x = Х к она будет
Но отличие γ(x) от чисто аддитивной погрешности состоит в том, что заметное возрастание γ(x) начинается тем позже, чем меньше γ н по сравнению с γ S. Для иллюстрации этого явления на рис. 1.6 изображены кривые возрастания γ(х) при уменьшении х при разных γ S /γ н для частного случая
Из этих кривых видно, как расширяется рабочий диапазон СИ по мере увеличения отношения γ S /γ н, т.е. уменьшения Δ o и приближения полосы погрешностей, приведённой на рис. 1.5, а, к чисто мультипликативной полосе (см. рис. 1.2, б). Так, если заданное значение погрешности γ з, ограничивающее нижнюю границу рабочего диапазона, принять в нашем примере γ з = 4%, то при γ S /γ н = 0, т. е. при γ S = 0 и чисто аддитивной полосе погрешностей, представленной на рис. 1.2, а, рабочий диапазон будет двукратным (от 50 до 100%). При γ S /γ н = 3 он становится уже пятикратным (от 20 до 100%), а при γ S /γ н = 20 – становится двадцатикратным (от 5 до 100%). В последнем случае в интервале от 100 до 10% диапазона прибора погрешность результатов измерения почти не изменяется, т. е. большие и малые значения измеряются с одной и той же относительной погрешностью. Форму полосы погрешностей, которая изображена на рис. рис. 1.5, а, а следовательно, и вытекающие из этого свойства имеют высокоточные потенциометры постоянного тока, цифровые вольтметры и другие высокоточные приборы. Формальным отличительным признаком для них является то, что их класс точности, согласно ГОСТ 8.401-80, обозначается не одним, а двумя числами, записываемыми через косую черту, т. е. в виде условной дроби γ к /γ н, в числителе которой указывается (в процентах) приведённая погрешность γ к в конце диапазона измерений, а в знаменателе – приведенная погрешность γ н в нуле диапазона.
Кроме перечисленных разновидностей нормирования погрешностей средств измерений (путём указания классов точности в виде γ S, γ 0, γ к / γ н), ГОСТ 8.401-80 разрешает использовать так называемые специальные формулы нормирования погрешностей. Дело заключается в том, что некоторые СИ не могут быть нормированы описанными выше способами, так как имеют более сложный вид полосы погрешностей, чем приведённый на рис. 1.2 и рис. 1.5, а. Это, например, цифровые частотомеры, погрешность которых зависит не только от измеряемой величины х, но и от времени Т, отводимого для измерения этой частоты. Мосты для измерения сопротивлений отличаются тем, что имеют не только нижний порог чувствительности (т. е. такое малое измеряемое сопротивление, когда погрешность достигает 100%, например, из-за неопределённости контактных сопротивлений), но и верхний порог чувствительности (когда погрешность при измерении очень больших сопротивлений вновь достигает 100%, например, из-за приближения измеряемого сопротивления к сопротивлению изоляции между зажимами самого моста). В этом случае погрешность результатов измерения описывается трёхчленной формулой вида
Во всех подобных случаях необходимо внимательно изучать документацию на соответствующий прибор и пользоваться для вычисления погрешности результата измерения приводимыми в ней специальными формулами.
Выраженные в процентах, они могут иметь значения 6 – 4 – 2,5 – 1,5 – 1,0 – 0,5 – 0,2 – 0,1 – 0,05 – 0,02 – 0,01 – 0,005 – 0,002 – 0,001 и т. д. Значение класса точности прибора маркируется на его шкале. Для того чтобы различить, какая из погрешностей обозначена в точности, используются следующие условные обозначения. Если класс точности прибора установлен по значению погрешности чувствительности γ; S, т.е. форма полосы погрешности условно принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком. Например, Если же полоса погрешностей принята аддитивной и прибор в качестве класса нормируется приведённой погрешностью нуля γ; 0 (таких приборов большинство), то класс точности указывается без каких-либо подчеркиваний (например, просто 1,5). Наконец, на приборах с резко неравномерной шкалой, например омметрах, класс точности прибора указывается в долях от длины шкалы и обозначается Обозначение класса точности в виде, например, 0,02/0,01 указывает, что погрешность прибора нормирована по двучленной формуле с γ; н = 0,01% и γ; к = 0,02%. Таким образом, обозначение класса прибора даёт достаточно полную информацию для вычисления приближённой оценки погрешностей результатов измерения.
Некоторые практические замечания по использованию нормируемых значений погрешности СИ для вычисления погрешности результатов измерения. Хотя ГОСТ 8.401-80 направлен на то, чтобы нормирование погрешностей СИ производилось единообразно, в измерительной практике такого единообразия пока ещё нет, так как используется большое число хороших высокоточных приборов, которые были выпущены ещё до введения этого стандарта, закупаются и широко используются приборы иностранного производства, нормированные, естественно, не в соответствии с ГОСТ 8.401-80, и т. д. Например, погрешность высокоточных потенциометров постоянного тока нормируется чаще всего двучленной формулой (1.1), а класс точности прибора указывается в виде одного числа – его относительной погрешности чувствительности. В этом случае указание класса точности в виде одного числа γ S не является признаком того, что прибор не имеет аддитивной составляющей погрешности, и потребитель обязан быть внимательным при расчёте погрешностей результатов измерения, чтобы не допустить ошибки. При нормировании погрешностей сложных СИ двучленной формулой (1.3) ГОСТ 8.401-80 предусматривает несколько иное ее написание, когда текущее значение относительной погрешности γ(х) выражается не через значение аддитивной γ; н и мультипликативной γ S составляющих предела допускаемых погрешностей, как в формуле (1.3), а через указываемые в обозначении класса точности приведенные погрешности в начале γ; н и в конце gк диапазона измерений. В этом случае, учитывая, что
Практически этим соотношением более удобно пользоваться для вычисления γ(x) по известным х, X к, γ; н и γ к, чем соотношением (1.3). У весьма широкодиапазонных приборов, например, мостов для измерения сопротивлений, в их технической документации вместо указания коэффициентов трёхчленной формулы (1.4) часто приводятся просто диапазоны, в которых погрешность результата измерения не превосходит указанного значения. Например, указывается, что относительная погрешность не превосходит: 0,5% в диапазоне от 10 2 до 10 4 Ом; 1% – от 5 до 10 5 Ом; 5% – от 0,5 до 10 6 Ом; 10% – от 0,2 до 2·10 6 Ом; 20% – от 0,1 до 4·10 6 Ом. Как правило, эти данные достаточно точно соответствуют трёхчленной формуле (1.4). Поэтому по ним можно определить коэффициенты Δ o, Δ ∞; и γ S формулы (1.4) и использовать её для аналитического определения γ(х) при любом произвольном значении х. Так, например, приведённым выше данным соответствует Δ o = 0,02 Ом, Δ ∞; = 20·10 6 Ом и γ S = 0,5%. Отсюда для любого х погрешность (в процентах)
|





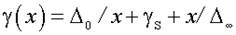 ,
,
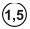 обозначает, что γ; S = 1,5%.
обозначает, что γ; S = 1,5%.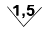 .
.