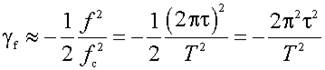Простейшая оценка динамических погрешностей результатов измерений
Всё рассмотренное выше относилось к определению статических погрешностей результатов измерений, когда предполагалось, что измеряемая величина остаётся во времени неизменной. На практике, однако, наоборот, сама потребность в измерении тех или иных величин чаще всего обусловлена тем, что они не остаются постоянными, а изменяются во времени. Принято говорить, что в этом случае речь идёт не об измерении той или иной величины, а об измерении процесса её изменения во времени. Так как результат измерения величины отражается числом, то результат измерения процесса представляет собой ряд последовательных чисел, отражающих значения измеряемой величины в последовательные моменты времени. Таким образом, результат измерения процесса в виде конечного набора чисел отражает этот процесс с каким-то приближением, т. е. с погрешностью. Эта погрешность носит название погрешности восстановления. Это название обусловлено тем, что, просто глядя на таблицу результатов, человек не может представить себе характер измеренного процесса. Он наносит полученные точки на график и по ним пытается восстановить характер этого процесса. Методы восстановления могут быть различными – точки можно соединить ступенчатой линией (кусочно-постоянная функция), прямыми (кусочно-линейная) или дугами парабол и т. д., и погрешность восстановления будет разной. Но совершенно ясно, что погрешность восстановления будет большой, если точки расположены во времени далеко друг от друга, и малой, если они расположены часто.
Выбор средств измерений по их быстродействию прежде всего определяется именно быстродействием, т. е. обеспечиваемой частотой дискретизации во времени. Её возможное наибольшее значение полностью определяется методом регистрации данных в используемой аппаратуре. Так, стрелочные показывающие приборы имеют время установления показаний 4 с плюс время записи результата наблюдателем (примерно 2 с), поэтому период дискретизации в этом случае t o ≥ 6 с. При использовании быстродействующих цифровых приборов и записи результатов наблюдателем в большинстве случаев можно считать t o ≥ 2 с, электрифицированная пишущая машинка обеспечивает скорость печати 7 знаков в секунду, но если каждый отсчёт регистрируется тремя десятичными цифрами плюс пробел, то t o ≈ 0,5 с. Более быстродействующими регистраторами на носитель, пригодный для ввода данных в ЭВМ, являются ленточные перфораторы ПЛ-80 (80 знаков в секунду) и ПЛ-150 (150 знаков в секунду). При регистрации на каждый отсчёт трёх десятичных знаков плюс пробел перфоратор ПЛ-80 позволяет регистрировать 80/4 = 20 отсчётов в секунду, а ПЛ-150, соответственно, 150/4 = 37,5 отсчёта в секунду, т. е. t o = 0,05 или t o = 0,027 с ≈ 0,03 с. Большую скорость регистрации данных могут обеспечить лишь быстродействующие АЦП, работающие совместно с ЭВМ. В этом случае t o может составлять, например, 30 мкс, т. е. обеспечивается регистрация 30 000 отсчётов в секунду. Наибольшее быстродействие достигается путём осуществления так называемого канала прямого доступа в память ЭВМ, минуя её процессор. В этом режиме, например, ЭВМ "Электроника-100" или "Электроника-60" обеспечивают ввод от 12- до 16-разрядных двоичных чисел, т. е. четырёхразрядных десятичных, с частотой 500 000 чисел в секунду. Для того чтобы получить представление о том, какие процессы и с какой погрешностью восстановления могут быть зарегистрированы при использовании перечисленных технических средств, рассмотрим пример. Предположим, что восстановление кривой процесса по зарегистрированным отсчётам производится методом линейной интерполяции, т. е. полученные точки просто соединяются между собой отрезками прямых линий. В этом случае плавные участки, близкие к прямым линиям, восстанавливаются с малыми погрешностями, а максимальная погрешность восстановления получается на участках с максимальной кривизной (рис. 1.7). Известно, что любую кривую х(t) на некотором участке можно разложить по степеням t, т. е. описать многочленом. В простейшем случае, используя лишь первые члены разложения, участок кривой между отсчётами можно представить в виде параболы, тогда погрешность линейной интерполяции будет представлять собой разность между этой параболой и её хордой, соединяющей смежные отсчёты. Как известно, парабола имеет наибольшее отклонение от хорды в середине интервала интерполяции t o с абсолютным значением (Δ m на рис. 1.7)
Отсюда максимальное значение погрешности восстановления наблюдается на участках кривой с наибольшей кривизной (в области максимумов и минимумов процесса на рис. 1.7). Если задать не абсолютную погрешность Δ m, а её приведённое значение
X к – предел измерений,
Так как любую сложную кривую можно разложить на ряд гармонических составляющих, определим необходимый период дискретизации для синусоидального процесса. При
Соотношение (1.7) воспринимается более наглядно, если из него вычислить число точек п, приходящихся на каждый период Т синусоидального процесса:
Таким образом, для восстановления синусоидального процесса с максимальной погрешностью 1% при равномерной дискретизации необходимо иметь 22 отсчёта на период процесса, но для представления с погрешностью 0,1% нужно не менее 70 отсчётов на каждый период, а для γ m = 20% достаточно пяти отсчётов на период. Исходя из соотношения (1.8), можно подсчитать минимальный период или максимальную частоту процесса, которые могут быть зарегистрированы с заданной максимальной погрешностью γ m разными из перечисленных выше средств. Данные о максимальных погрешностях приведены в табл. 1.1 и свидетельствуют о том, что без использования ЭВМ или специальных самописцев, магнитописцев или осциллографов могут быть зарегистрированы лишь очень медленные процессы (с периодом 0,2 – 2 с).
Из выражения (1.7) или (1.8) получаем
т. е. динамическая погрешность восстановления γ m возрастает с квадратом частоты восстанавливаемого процесса.
Рассмотрим это свойство погрешности восстановления на конкретном примере. Так, в табл. 1.1 указано, что при использовании АЦП с периодом дискретизации t 0 = 30 мкс исследуемый процесс с частотой f 1 = 500 Гц восстанавливается с γ m1 ≈ 0,1%. Действительно, рассчитывая γ m1 по формуле (1.9), получаем
Однако если в кривой этого процесса содержится дополнительно ещё 10-я гармоника с частотой f 10 = 5 000 Гц и амплитудой в 0,1 основной волны, она будет восстанавливаться с относительной погрешностью γ m10 в 100 раз большей, чем γ m1, т. е. равной 10%. Правда, так как амплитуда этой гармоники в 10 раз меньше амплитуды основной волны, то приведённое значение этой погрешности составит лишь γ m10 = 1%. Тем не менее, результирующая погрешность восстановления всего процесса будет в 10 раз (!) больше, чем погрешность восстановления γ m1 = 0,1% процесса, не содержащего этой высокочастотной составляющей. Погрешность восстановления для основной волны и её гармоник является систематической (она всегда отрицательна, см. рис. 1.7, и приводит к уменьшению восстанавливаемой амплитуды кривой), однако если высокочастотная составляющая вызвана шумом или другими помехами и не синхронна с основной волной, то и погрешность восстановления оказывается случайной и наблюдается в виде случайного разброса отсчётов. При ручной регистрации наблюдений подобный разброс данных будет сразу замечен экспериментатором, и он примет соответствующее решение о ходе эксперимента. Рассмотренное явление особенно опасно при автоматическом вводе данных в ЭВМ и подчеркивает крайнюю важность метрологического анализа динамических погрешностей в этом случае.
Поэтому для регистрации процессов, протекающих с частотами от 1 Гц до 5 – 50 кГц, широко используются аналоговые средства регистрации: самопишущие приборы с чернильной записью, светолучевые и электронные осциллографы с фотоприставками. Динамические погрешности таких приборов, а также используемых в комплекте с ними датчиков и усилителей принято нормировать указанием их амплитудно-частотной характеристики, представляющей собой график зависимости от частоты f отношения их чувствительности S при частоте f к чувствительности S при f = 0 (см. ГОСТ 8.256-77). В большинстве случаев эти характеристики имеют вид кривых, показанных на рис. 1.8. При апериодической частотной характеристике (рис. 1.8, а) (показывающие приборы, усилители, датчики температуры и т. п.) чувствительность S прибора или датчика монотонно понижается с ростом частоты f воспринимаемого процесса. Частотная погрешность γ f есть разность между ординатами частотной характеристики и постоянным уровнем S / S 0 = 1, показанным на рис. 1.8, а штриховой прямой. Она всегда отрицательна и увеличивается с ростом частоты f. Её численное значение может быть найдено из этого графика для любой частоты и использовано для оценки точности регистрации или введения поправки в результат измерения. Частотная характеристика, изображенная на рис. 1.8, б, характерна для колебательных систем с малым успокоением (гальванометров, светолучевых осциллографов, датчиков манометров, акселерометров и т. д.). Она имеет резонансный пик вблизи собственной частоты f 0 колебательной системы и положительную частотную погрешность γ f. Для приборов и датчиков с такими частотными характеристиками нормируется рабочий диапазон частот, простирающийся от f = 0 до такой частоты f гр, где γ; f достигает некоторого граничного значения γ; fгр. Так как граничное значение частотной погрешности достигается только в конце рабочего диапазона частот, то внутри его частотные погрешности оказываются намного меньше этого значения. Располагая частотной характеристикой прибора или датчика, можно найти частотную погрешность для любого значения частоты регистрируемого процесса внутри рабочего диапазона частот. Так, например, при частотной характеристике, приведенной на рис. 1.8, б, частотная погрешность может быть рассчитана по формуле
где β – степень успокоения колебательной системы; f 0 – её собственная частота. При отсутствии успокоения (β ≈ 0), что характерно для датчиков, не имеющих специальных средств успокоения, частотная погрешность
Для них частотная погрешность может быть приближённо выражена как
Полагая, что степень успокоения датчика β ≈ 0, и используя соотношение (1.11), получаем, что при частоте измеряемого процесса f = 50 Гц его частотная погрешность γ; f = 0,01%, но при f = 100 Гц уже γ; f = 0,04%, при f = 500 Гц γ; f = 1%, а при f = 1 000 Гц γ; f = 4%, т. е. рабочий диапазон частот датчика оказывается уже исчерпанным.
Для этого преобразуем формулу (1.12), заменив f на 1/Т, где Т – период измеряемого процесса; тогда получим
Соотношения (1.11) и (1.12) показывают, что частотная погрешность возрастает пропорционально квадрату частоты, что, как и при дискретных отсчётах, приводит к очень неблагоприятным соотношениям при регистрации несинусоидальных процессов. Поэтому изложенные выше предостережения остаются актуальными и в этом случае.
|

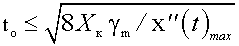 .
.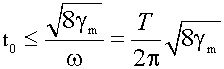
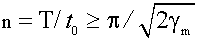
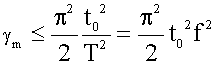
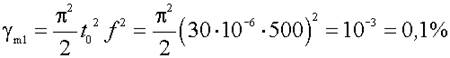 ,
,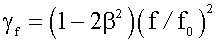
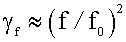
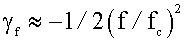
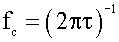 – так называемая частота среза частотной характеристики;
– так называемая частота среза частотной характеристики;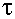 – постоянная времени.
– постоянная времени.