Правила округления значений погрешности и результатов измерений
Рассчитывая значения погрешности по формулам (1.5) и (1.6), особенно при пользовании электронным калькулятором, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчёта являются нормируемые значения погрешности СИ, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна-две значащие цифры. При этом приходится учитывать следующее. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 – 50%), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т. е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности. Исходя из этого, на практике установилось такое правило: если полученное число начинается с цифры, равной или большей
Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, – если первая есть 3 и более. Результат измерения округляется до того же десятичного разряда, которым оканчивается округлённое значение абсолютной погрешности. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.
На вольтметре класса точности 2,5 с пределом измерений 300 В был получен отсчёт измеряемого напряжения х = 267,5 В. Расчёт погрешности удобнее вести в следующем порядке: сначала необходимо найти абсолютную погрешность, а затем – относительную. Абсолютная погрешность
относительная
Так как первая значащая цифра значения абсолютной погрешности (7,5 В) больше трёх, то это значение должно быть округлено по обычным правилам округления до 8 В, но в значении относительной погрешности (2,81%) первая значащая цифра меньше 3, поэтому здесь должны быть сохранены в ответе два десятичных разряда и указано γ(x) = 2,8%. Полученное значение x = 267,5 В должно быть округлено до того же десятичного разряда, которым оканчивается округлённое значение абсолютной погрешности, т. е. до целых единиц вольт. Таким образом, в окончательном ответе должно быть сообщено: "Измерение произведено с относительной погрешностью γ(x) = 2,8%. Измеренное напряжение х = (268 ± 8) В или х = 268 В ± 8 В". При этом более наглядно указать пределы интервала неопределённости измеренной величины в виде х = 260 ÷ 276 В или 260 В < х < 276 В. Наряду с изложенными правилами округления значений погрешностей результатов измерения, иногда (например, в [3]) предлагаются более обоснованные, но и более сложные правила. Недостаток изложенных правил состоит в том, что относительная погрешность от округления изменяется скачком при переходе, например, от числа 0,29, когда она составляет (0,30 – 0,29) / 0,30 = 3%, к числу 0,3, когда она будет (0,4 – 0,3)/0,3 = 30%. Для устранения столь резкого скачка относительной погрешности округления предлагается каждую декаду возможных значений округляемой погрешности делить на три части: от 0,1 до 0,2; от 0,2 до 0,5 и от 0,5 до 1,0; и в каждой из этих частей использовать свой шаг округления, соответственно, равный 0,02; 0,05 и 0,1. Тогда ряд разрешённых к употреблению округлённых значений погрешностей получает вид: 0,10 – 0,12 – 0,14 – 0,16 – 0,18 – 0,20 – 0,25 – 0,30 – 0,35 – 0,40 – 0,45 – 0,5 – 0,6 – 0,7 – 0,8 – 0,9 – 1,0. Бесспорное преимущество такого ряда состоит в том, что погрешность от округления на границах участков изменяется лишь от 5 до 10%. Однако при использовании такого правила округления погрешности последние цифры результата, оставляемые после округления, также должны соответствовать приведённому ряду.
|

 , то в нём сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нём сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5% указываются два знака, но в числах 0,5; 4; 6% указывается лишь один знак.
, то в нём сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нём сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5% указываются два знака, но в числах 0,5; 4; 6% указывается лишь один знак.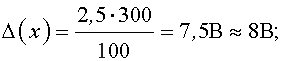
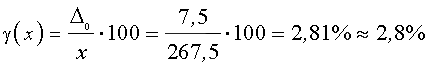 .
.


