СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
ОСНОВЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
ИЗМЕРЕНИЯ И ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
В каждой лабораторной работе по курсу "Физика" студент измеряет одну или несколько величин. Измерение называется прямым, если измеряемая величина непосредственно сравнивается с эталоном. Такое сравнение, как правило, происходит с помощью измерительного прибора. Например, длина тела измеряется с помощью микрометра или штангенциркуля, сила тока измеряется амперметром и т.д. Результат косвенного измерения является известной функцией величин, получаемых с помощью прямых измерений. В процессе прямого измерения получают ряд наблюдений х1, х2, …, хn измеряемой величины х. Результаты отдельных наблюдений содержат погрешности измерений и нуждаются в дополнительной обработке. Виды погрешностей: случайные, систематические, промахи.
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
При наличии случайных погрешностей результат отдельного наблюдения хk измеряемой величины х является случайной величиной. В этом случае результаты наблюдений х1, х2, …, хn одной и той же величины х различны. В качестве результата измерения принимается среднее арифметическое значение результатов наблюдений:
Предел результата измерения при n®¥ называется математическим ожиданием m:
Случайную величину х, являющуюся результатом отдельного наблюдения, можно задать с помощью функции распределения f(х) (функции плотности вероятности):
где dP - вероятность попадания случайной величины в интервал Если случайная величина зависит от большого количества неконтролируемых изменяющихся причин, то она подчиняется нормальному распределению или распределению Гаусса. Функция распределения Гаусса для случайной величины х с математическим ожиданием m описывается формулой:
где
С учетом формулы (1.3) вероятность Р попадания результата наблюдения х в интервал (х1, х2) равна
Рассмотрим интервал, в центре которого находится математическое ожидание m, а полуширина равна
где
Вычисление интеграла в формуле (1.6) показывает, что при Пусть наличие случайных погрешностей приводит к тому, что результат наблюдения х измеряемой величины подчиняется нормальному распределению. Параметры m и s этого распределения экспериментатор не знает. В процессе измерения получают n результатов наблюдений: х1, х2, …, хn, т.е. получают некоторую выборку значений х из генеральной совокупности допустимых значений. Определяя результат измерения
где S(х) - выборочная оценка стандартного отклонения результата наблюдения; n - число наблюдений. Если результат отдельного наблюдения х является случайной величиной, подчиняющейся нормальному распределению с дисперсией D(х), то результат измерения
Теоретически показано, что для каждой вероятности Р (меры доверия) можно построить такой доверительный интервал (
где S(
При наличии только случайных погрешностей запись результата измерения:
|

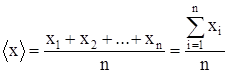 . (1.1)
. (1.1)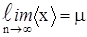 . (1.2)
. (1.2)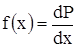 или
или 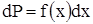 , (1.3)
, (1.3) , (1.4)
, (1.4)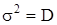 - дисперсия распределения. Величина
- дисперсия распределения. Величина 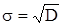 называется стандартным или среднеквадратичным отклонением. График функции распределения Гаусса показан на рис.1.
называется стандартным или среднеквадратичным отклонением. График функции распределения Гаусса показан на рис.1.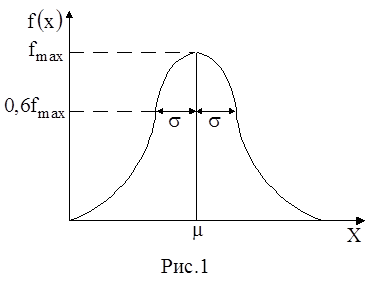 Математическое ожидание m определяет положение оси симметрии кривой распределения, а величина s характеризует разброс х относительно m.
Математическое ожидание m определяет положение оси симметрии кривой распределения, а величина s характеризует разброс х относительно m.
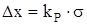 , (1.5)
, (1.5)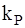 - некоторое число. Вероятность Р наблюдения случайной величины х, подчиняющейся нормальному распределению, в таком интервале определяется формулой:
- некоторое число. Вероятность Р наблюдения случайной величины х, подчиняющейся нормальному распределению, в таком интервале определяется формулой: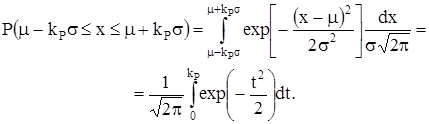 (1.6)
(1.6)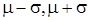 ). Соответственно, при kP = 2,0 получим Р = 0,95, а при kP = 3,0 вероятность Р = 0,997.
). Соответственно, при kP = 2,0 получим Р = 0,95, а при kP = 3,0 вероятность Р = 0,997.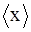 по формуле (1.1), находят выборочную оценку величины m. Выборочную оценку дисперсии нормального распределения результатов наблюдений получают по формуле
по формуле (1.1), находят выборочную оценку величины m. Выборочную оценку дисперсии нормального распределения результатов наблюдений получают по формуле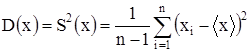 , (1.7)
, (1.7)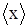 , определяемый по формуле (1.1), также подчиняется нормальному распределению с дисперсией
, определяемый по формуле (1.1), также подчиняется нормальному распределению с дисперсией 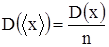 . Соответственно, выборочная оценка стандартного отклонения результата измерения равна
. Соответственно, выборочная оценка стандартного отклонения результата измерения равна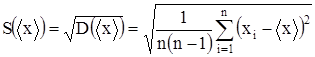 . (1.8)
. (1.8)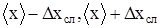 ), что математическое ожидание m случайной величины х окажется внутри этого интервала с вероятностью Р. Полуширина такого доверительного интервала определяется формулой:
), что математическое ожидание m случайной величины х окажется внутри этого интервала с вероятностью Р. Полуширина такого доверительного интервала определяется формулой: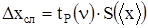 , (1.9)
, (1.9)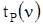 - коэффициент Стьюдента, величина которого зависит от вероятности Р и числа степеней свободы n (см. таблицу Приложения). Число степеней свободы n связано с числом наблюдений n формулой:
- коэффициент Стьюдента, величина которого зависит от вероятности Р и числа степеней свободы n (см. таблицу Приложения). Число степеней свободы n связано с числом наблюдений n формулой: 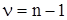 . Можно показать, что в формуле (1.5) коэффициент
. Можно показать, что в формуле (1.5) коэффициент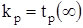 . (1.10)
. (1.10) .
.


