СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
Величину некоторых систематических погрешностей можно определить теоретически или экспериментально. Такие оценки называются поправками. Результаты наблюдений исправляют на величину поправок. Но существуют такие систематические погрешности (например, погрешность измерительного прибора, погрешность округления и др.), которые нельзя найти в виде поправки. Погрешность измерительного прибора задается в виде предельной или абсолютной погрешности d или относительной погрешности g (класса точности прибора). Класс точности g прибора - это выраженное в процентах отношение предельной погрешности прибора d к максимальному значению хmax измеряемой величины:
В частности, для электроизмерительных приборов существуют восемь классов точности: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 2,5; 4,0. Отсюда предельное значение абсолютной погрешности:
Итак, погрешность прибора дается в виде предельного значения d. В случае нормального распределения вероятность наблюдения величины х, для которой Отсюда, Тогда, учитывая формулы (1.5), (1.10) и (1.11), ширину доверительного интервала систематической погрешности прибора можно записать в виде:
При измерении совершается погрешность округления. Если цена деления шкалы прибора равна h, то предельная ошибка округления равна h/2. Можно показать, что полуширина доверительного интервала, связанного с погрешностью округления, определяется формулой
где Р - доверительная вероятность. В некоторых случаях ошибка измерения связана с субъективной реакцией экспериментатора. Например, при измерении промежутка времени ручным секундомером возникает ошибка, вызванная запаздыванием реакции экспериментатора. Можно показать [5], что стандартное отклонение субъективной реакции В соответствии с формулой (1.5) полуширина доверительного интервала равна
|

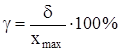 .
.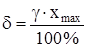 .
. >3s, равна 0,3%, т.е. отклонение 3s от среднего можно считать значением 3s=d.
>3s, равна 0,3%, т.е. отклонение 3s от среднего можно считать значением 3s=d. . (1.11)
. (1.11)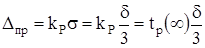 . (1.12)
. (1.12)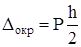 , (1.13)
, (1.13) с.
с.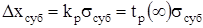 . (1.14)
. (1.14)


