ГЛАВА 3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ
Необходимо определить в простой кейнсианской модели формирования доходов параметры уравнения функции потребления. Исходная система уравнений имеет вид:
Yt=Ct+It (20) где t – индекс, указывающий на то, что уравнения (4), (5) являются системой одновременных уравнений для моментов времени t1 – tn; ut – случайная составляющая. Ct, Yt - эндогенные переменные функции потребления и дохода, соответственно. Напрямую из уравнения (4) методом наименьших квадратов (МНК) найти параметры a и b невозможно, так как оценки будут смещенными. Необходимо использовать косвенный метод наименьших квадратов (КМНК). Для этого эндогенные переменные выразим через экзогенные. Подставим выражение (19) в (20): Yt = a+bYt + ut +It,(21)
отсюда имеем:
Подставим Yt в уравнение (19) и получим:
Данное уравнение не содержит в правой части эндогенных переменных, а имеет только экзогенную переменную в виде It (инвестиций). Экзогенная переменная не коррелирует со случайной составляющей ut и, следовательно, параметры этого уравнения могут быть найдены с помощью МНК. Представим это уравнение в следующем виде: Ct= a*+b*It + ut*,
где
Используя имеющиеся в таблице 2 в соответствии с заданным вариантом данные о величинах Ct и It, найдем с помощью МНК несмещенные оценки a* и b* из уравнения: Ct = a1+b1 It, (25) где a1 - несмещенная оценка a*; b1- несмещенная оценка b*. Для этих целей применим, имеющийся в табличном редакторе Excel пакет прикладных программ, реализующий определение параметров уравнения регрессии методом наименьших квадратов. Активизация этого метода производится командами: “ Сервис” – “Анализ данных” – “Регрессия”.
После определения значений a1 и b1 необходимо определить несмещенные оценки величин a и b, использовав соотношения:
где a", b" – соответственно, несмещенные оценки a, b. Сами значения величин a", b" необходимо определить по формулам:
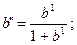 (27) (27)
a”=150205 b”=0,547047 Использовав найденные значения a" и b", записываем уравнение функции потребления (19) C(t)= 150205+0,547047+ut Сравниваем найденные по формуле (27) значения a” и b” с величиной a и b, заданными в таблице 1 вариантов заданий. Расчитываем проценты несовпадения данных величин по формулам:
Определяем по формуле (20) значения величин Yt (для t в пределах от t1 до t14), взяв значения Ct и It из таблицы 2 вариантов заданий.
Приняв в качестве исходных данных имеющиеся значения Ct и Yt, определяем с помощью метода наименьших квадратов смещенные оценки aсм и bсм величин a и b, используя уравнение (19). Сравниваем найденные значения aсм и bсм с величиной a и b, заданными в таблице 1 вариантов заданий. Расчитываем проценты несовпадения данных величин по формулам:
Сравниваем проценты несовпадения, полученные по формулам (28) и (29).
|

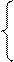 Ct= a+bYt + ut; (19)
Ct= a+bYt + ut; (19)
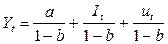 (22)
(22)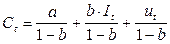 (23)
(23)

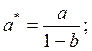

 (24)
(24)
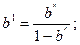 (26)
(26)





