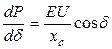Статическая устойчивость простейшей системы
Под простейшей системой понимается такая, в которой одиночная электростанция (эквивалентный генератор) связана с шинами (системой) неизменного напряжения трансформаторами и линиями, по которым передается мощность от станции в систему (рисунок 10.1, а). Принимается, что суммарная мощность электрических станций системы во много раз превышает мощность рассматриваемой станции. Это позволяет считать напряжение на шинах системы неизменным (U= const) при любых режимах ее работы. На рисунок 10.1, б представлены два основных агрегата тепловой электрической станции: турбина и генератор. Ротор турбины приводится во вращение паром, подводимым к турбине от котла электростанции. Вращающий момент турбины зависит от количества энергоносителя. Для паровой турбины - это пар, для гидротурбин - вода. В нормальном режиме эксплуатации основные параметры энергоносителя - температура и давление пара - стабильны, поэтому вращающий момент турбины постоянен. Мощность, выдаваемая генератором в систему, определяется несколькими параметрами, влияние которых зависит от характеристики мощности генератора.
Рисунок 10.1. Оценка статической устойчивости простейшей системы:
а) принципиальная схема системы; б) блок турбины – генератор; в) векторная диаграмма генератора; г) схема замещения системы; д) механический аналог блока турбина – генератор;
Из векторной диаграммы следует, что Зависимость имеет синусоидальный характер и называется характеристикой мощности генератора. При постоянных ЭДС Е генератора и напряжении U угол поворота генератора определяется только его активной мощностью, которая, в свою очередь, определяется мощностью турбины. Наглядной иллюстрацией зависимости мощности (момента) турбины от угла сдвига δ является система двух дисков, соединенных пружинами (рисунок 10.1, д). В режиме холостого хода (без учета трения) приводящий (поле ротора, связанного с турбиной) и приводимый (поле статора) диски не образуют угла сдвига относительно друг друга. При появлении тормозящего момента (реакция статора) угол сдвига между диска будет тем больше, чем больше тормозящий момент. Очевидно, что при увеличении тормозящего момента может произойти поворот одного диска относительно другого, что является нарушением устойчивости рассматриваемой системы. Мощность турбины зависит от количества энергоносителя, и в координатах Р, δ изображается прямой линией. При определенных значениях ЭДС генератора Е и напряжения приемной системы U характеристика мощности имеет максимум, который вычислялся по формуле Механическим аналогом рассматриваемой системы с точки зрения статической устойчивости может служить шарик, помещенный на изогнутую поверхность так, как это показано на рисунке 10.1, г. Положение точки а устойчиво, так как любое (даже незначительное) перемещение шарика влево или вправо заканчивается его возвращением в исходную точку. Положение b неустойчиво, Так как малейшее отклонение от этого положения вызовет переход шарика в новое положение. Формальным признаком статической устойчивости электрической системы может служить знак приращения мощности к приращению угла. Если ∆Р/∆δ > 0, то система устойчива, если это соотношение отрицательно, то неустойчива. Переходя к пределу, можно записать критерий устойчивости простейшей системы:
Запас устойчивости электропередачи, связывающей станцию с шинами энергосистемы, должен быть не менее 20 % в нормальном режиме и 8 % в кратковременном послеаварийном. В рассматриваемых простейших условиях признаком устойчивости системы является такой характер изменения мощностей и моментов при небольшом отклонении от состояния равновесия, который вынуждает систему вновь возвращаться к исходному состоянию. В режиме работы в точке а (рисунок 10.2), мощности генератора и турбины уравновешивают друг друга. Если допустить, что угол Под влиянием тормозящего момента ротор генератора начинает замедляться, что обусловливает перемещение связанного с ротором вектора э.д.с. генератора Е в сторону уменьшения угла
Совершенно иной получается картина в точке b. Здесь положительное приращение угла Изменение мощности генератора вызывает появление избыточного момента ускоряющего характера, под влиянием которого угол Под статической устойчивостью, вообще говоря, понимают способность системы самостоятельно восстановить исходный режим работы при малом возмущении. Статическая устойчивость является необходимым условием существования установившегося режима работы системы, но отнюдь не предопределяет способности системы продолжать работу при резких нарушениях режима, например при коротких замыканиях. Итак, точка а и, любая другая точка на возрастающей части синусоидальной характеристики мощности отвечают статически устойчивым режимам и, наоборот, все точки падающей части характеристики — статически неустойчивым. Отсюда вытекает следующий формальный признак статической устойчивости рассмотренной простейшей системы: приращения угла
Производная
Она положительна при Метод малых отклонений, или малых колебаний широко используется при анализе устойчивости системы. Следует отметить, что причиной нарушения статической устойчивости может быть работа автоматики при ошибке в установке регулировочных коэффициентов или выходе режима за пределы зоны устойчивости. Рекомендуемая литература: ОЛ3, ДЛ1 Контрольные вопросы 1. Что называется статической устойчивостью? 2. Что называется пропускной способностью? 3. Что такое позиционная система? 4. Что представляет собой статические характеристики? 5. Перечислите основные задачи устойчивости электрических систем? 6. Какие допущения принимается при анализе устойчивости? 7. Что понимается под статической устойчивостью электрической системы? 8. Как осуществляется учет АРВ пропорционального и сильного действия в приближенных расчетах статической устойчивости? 9. По каким параметрам ведется регулирование тока возбуждения генератора при наличии АРВ пропорционального или сильного действия? 10. Объясните механизм повышения предела статической устойчивости энергосистемы при использовании АРВ пропорционального и сильного действия? 11. Назовите средства повышения статической устойчивости энергосистемы и объясните механизм их действия?
|

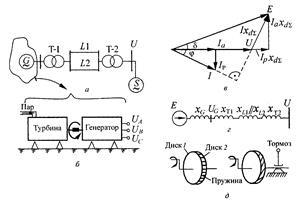
 Для получения характеристики мощности построена векторная диаграмма электропередачи (рисунок 10.1, в). Она повторяет диаграмму, однако в ней полный вектор тока заменен на его действительную и мнимую составляющие, а сопротивление xd - на сопротивление хdΣ получаемое из схемы замещения системы, представленной на рисунок 10.1, г:
Для получения характеристики мощности построена векторная диаграмма электропередачи (рисунок 10.1, в). Она повторяет диаграмму, однако в ней полный вектор тока заменен на его действительную и мнимую составляющие, а сопротивление xd - на сопротивление хdΣ получаемое из схемы замещения системы, представленной на рисунок 10.1, г: 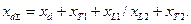
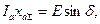 где I а - активная составляющая тока; δ - угол сдвига ЭДС E относительно напряжения U. Умножая обе части равенства на U/хdΣ получим
где I а - активная составляющая тока; δ - угол сдвига ЭДС E относительно напряжения U. Умножая обе части равенства на U/хdΣ получим 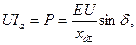 где Р - активная мощность, выдаваемая генератором (принята в относительных единицах).
где Р - активная мощность, выдаваемая генератором (принята в относительных единицах).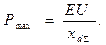 Иногда эту величину называют «идеальным» пределом мощности простейшей электрической системы. Заданному значению мощности турбины соответствуют две точки пересечения характеристик а и b, в которых мощности генератора и турбины уравновешивают друг друга.
Иногда эту величину называют «идеальным» пределом мощности простейшей электрической системы. Заданному значению мощности турбины соответствуют две точки пересечения характеристик а и b, в которых мощности генератора и турбины уравновешивают друг друга.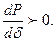 Увеличение мощности турбины от значения Р0 до Р/0 приводит к возрастанию угла ротора до значения
Увеличение мощности турбины от значения Р0 до Р/0 приводит к возрастанию угла ротора до значения 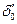 и уменьшению запаса статической устойчивости, который определяется следующим образом:
и уменьшению запаса статической устойчивости, который определяется следующим образом: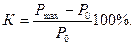
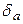 получает небольшое приращение
получает небольшое приращение 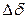 , то мощность генератора, следуя синусоидальной зависимости от угла, также изменится на некоторую величину
, то мощность генератора, следуя синусоидальной зависимости от угла, также изменится на некоторую величину 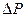 , причем, как видно из рисунке 10.2, в точке а положительному приращению угла
, причем, как видно из рисунке 10.2, в точке а положительному приращению угла 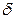 и при любых изменениях последнего остается постоянной и равной
и при любых изменениях последнего остается постоянной и равной 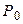 . В результате изменения мощности генератора равновесие моментов турбины и генератора оказывается нарушенным и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора в силу положительного изменения мощности
. В результате изменения мощности генератора равновесие моментов турбины и генератора оказывается нарушенным и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора в силу положительного изменения мощности 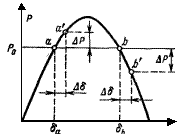 Рисунок 10.2. Изменение мощности при приращениях угла
Рисунок 10.2. Изменение мощности при приращениях угла
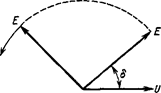 Рисунок 10.3. Выпадение из синхронизма
Рисунок 10.3. Выпадение из синхронизма
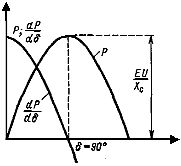 Рисунок 10.4. Зависимость синхронизирующей мощности от угла
Рисунок 10.4. Зависимость синхронизирующей мощности от угла
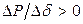 или, переходя к пределу:
или, переходя к пределу: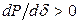
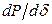 , как известно, носит название синхронизирующей мощности, и, следовательно, критерием статической устойчивости системы в рассмотренных условиях является положительный знак синхронизирующей мощности. Производная мощности по углу согласно (2.1) равна:
, как известно, носит название синхронизирующей мощности, и, следовательно, критерием статической устойчивости системы в рассмотренных условиях является положительный знак синхронизирующей мощности. Производная мощности по углу согласно (2.1) равна: