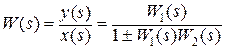Динамические звенья и структурные схемы САР
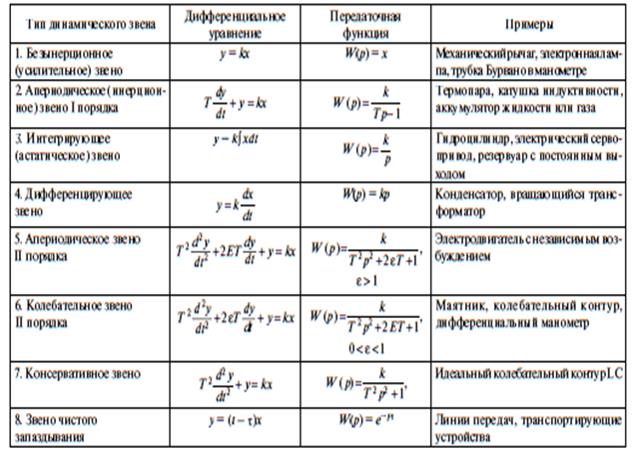
Для математического описания динамики САР и анализа ее работы систему удобно рассматривать не в виде совокупности отдельных связанных между собой элементов автоматики, а разбивать на динамические звенья. Под элементарным динамическим звеном понимается искусственно выделяемая часть автоматической системы, которая характеризуется определенными динамическими свойствами и описывается дифференциальным уравнением не выше второго порядка. В отличие от элемента автоматики динамическое звено не обязательно являются конструктивно или схемно оформленных устройством. Одним элементарным динамическим звеном могут быть представлены несколько элементов системы или, наоборот, один элемент может быть представлен в виде нескольких звеньев. Каждое динамическое звено характеризуется следующими динамическими показателями: уравнением динамики, передаточной функцией, переходной, частотной и импульсной характеристиками. В зависимости от вида дифференциального уравнения различают следующие типовые динамические звенья: пропорциональное (усилительное), апериодическое, интегрирующее, дифференцирующее, колебательное, чистого запаздывания, дифференциальные уравнения (табл. 1.1). Таблица 1.1. Типовые динамические звенья
Замена элементов САР соответствующими динамическими звеньями позволяет получить динамическую модель системы. Соединение звеньев ее модели должно соответствовать соединению элементов системы. Графическое изображение САР в виде соединенных определенным образом динамических звеньев называется структурной схемой автоматической системы. Структурная схема отображает динамические свойства системы и представляет по существу графическое изображение уравнений динамики элементов в виде передаточных функций. Представление САР структурными схемами, составленными из динамических звеньев, облегчает задачу нахождения общей передаточной функции и уравнения динамики системы в целом, а также дает возможность создать общие методы исследования для всех систем, независимо от их конструкции, физической природы и т.д.
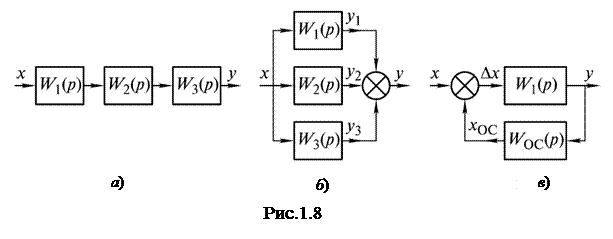
Для получения обобщенной передаточной функций пользуются правилами преобразования передаточных функций динамических звеньев, которые определяются видом их соединения. Существует три основных типа соединений динамических звеньев: последовательное, параллельное и встречно-параллельное или соединение с обратной связью (рис. 1.8). При последовательном соединении (рис. 1.8, а) выходная величина предыдущего звена является исходной величиной для последующего, а результирующая передаточная функция равна произведению передаточных функций звеньев:
При параллельном соединении (рис. 1.8, б) звеньев входная величина является общем для всех звеньев, выходная – равная алгебраической сумме выходных величин звеньев, а передаточная функция системы равна сумме передаточных функций звеньев:
Пердаточная функция системы с обратной связью (рис. 1.5, в) определяется по выражению
где плюс соответствует отрицательной обратной связи, а минус – положительной. Из формулы видно, что положительная обратная связь приводит к увеличению передаточной функции и применяется в основном в усилительных элементах и схемах. Отрицательная обратная связь ведет к уменьшению передаточной функции и используется в схемах для сохранения их состояния..
|

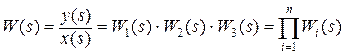 .
.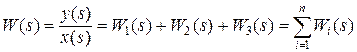 .
.