Устойчивость и качество процессов регулирования
Автоматическая система регулирования устойчива, если она, будучи выведенной из состояния установившегося движения (или покоя) некоторой причиной, приходит вновь в это состояние или в новое установившееся движение после прекращения действия этой причины. Устойчивость является одной из основных характеристик САР. Оно неразрывно связано со свободным движением системы, которое описывается однородным дифференциальным уравнением вида
Поэтому заключение об устойчивости системы можно сделать, проанализировав его решение, которое записывается в виде
где Сk, Сi, j i - постоянные интегрирования определяемые начальными условиями; a k -вещественные корни и a i ± jwi - комплексно-сопряженные корни характеристического уравнения ansn + an-1sn- 1 + …+ a 1 s + 1 = 0. Если все вещественные корни и вещественные части комплексных корней отрицательные, то с течением времени D y ® 0. Если хотя бы один из корней или вещественная часть комплексного корня окажутся положительными, то с течением времени D Y будет неограниченно возрастать, а следовательно, система будет неустойчивой.. Таким образом, необходимым и достаточным условием устойчивости САР является, чтобы все вещественные части корней характеристического уравнения были отрицательны. В настоящее время применяется ряд методов определения устойчивости, которые позволяют не только определить, устойчива или неустойчива система, но и дают рекомендации по обеспечению ее устойчивости или увеличению запаса устойчивости. Эти методы получили название критериев устойчивости. Для анализа систем применяют алгебраические, частотные, логарифмические и др. критерии устойчивости. К алгебраическим критериям устойчивости относятся критерии Раусса, Гурвица, Вышнеградского. Широкое распространение получил критерий устойчивости Гурвица, согласно этому критерию для устойчивости САР необходимо и достаточно, чтобы при всех положительных коэффициентах ai характеристического уравнения определитель Гурвица
и все его диагональные миноры
были положительны. Главный определитель Гурвица составляется из коэффициентов характеристического уравнения, начиная с главной диагонали. Критерий Гурвица рационально применять длдя анализа устойчивости САР, описываемых уравнениями не выше пятого порядка. Алгебраические критерии устойчивости позволяют установить только факт устойчивости системы, в то время как частотные критерии позволяют достаточно наглядно оценить степень устойчивости. К частотным критериям устойчивости относятся критерии Михайлова и Найквиста. Критерий Михайлова позволяет судить об устойчивости по кривой Михайлова, которую описывает конец вектора
при изменении w от 0 до
Критерий Найквиста основан на рассмотрении амплитудно-фазовых характеристик (АФЧХ) разомкнутой системы, по виду которой судят об устойчивости соответствующей замкнутой системы. АФЧХ разомкнутой системы может быть получена как аналитически, так и экспериментально, что выгодно отличает критерий Найквиста от ранее изложенных. Для анализа устойчивости здесь используется функция вида
где
При изменении w от 0 до
На основании изложенного критерий устойчивости Найквиста может быть сформулирован следующим образом. Замкнутая САУ устойчива, если при изменении
Для большинства САР, применяемых в строительстве, статическая ошибка регулирования составляет 3-5%. Перерегулирование D ymax - максимальное отклонение регулируемой величины от нового установившегося значения в переходном процессе. Величину перерегулирования обычно оценивают в относительных единицах
Перерегулирование является динамической ошибкой системы и не должна превышать допустимых значений. Для большинства строительных машин перерегулирование вообще не допустимо. Время регулирования t р определяется интервалом времени, прошедшим с момента изменения внешнего воздействия до момента, при котором отклонение регулируемой величины от установившегося значения не превышает допустимой величины e. Время регулирования оценивает длительность переходного процесса и характеризует быстродействие САР. Характер переходного процесса определяется числом колебаний регулируемой величины y за время переходного процесса t р и декрементом затухания. По виду переходные процессы могут быть (рис.1.8) колебательными (кривая 1), апериодическими (кривая 2), монотонными (кривая 3). При колебательном процессе регулируемая величина стремится к новому значению, совершая относительно него затухающие гармонические колебания. Причем отклонения повторяются с определенной частотой. Скорость затухания хаарктеризуется логарифмическим декрементом затухания
Апериодический процесс представляет собой промежуточный вид переходного процесса, при котором регулируемая величина стремится к новому установившемуся значению, совершая колебания относительно экспоненциальной кривой. Причем при апериодическом процессе регулируемая величина в процессе колебаний не выходит за установившееся значение. При монотонном процессе регулируемая величина плавно приближается к своему новому установившемуся значению. Такой вид переходных процессов обычно требуется в системах регулирования строительными процессами, подъемно транспортными и землеройными машинами. Для определения показателей качества регулирования необходимо построить кривую переходного процесса. Существуют различные аналитические и графоаналитические методы построения. Широко применяется экспериментальный метод получения кривой переходного процесса путем компьютерного моделирования. Стараются так подобрать параметры элементов системы, чтобы статическая ошибка, перерегулирование, время регулирования и запас устойчивости удовлетворяли требованиям, предъявляемым условиям эксплуатации системы. Если эту задачу не удается решить только за счет изменения параметров основных элементов системы, то в нее вводят корректирующие элементы. Устойчивость и качество процесса регулирования (время переходного процесса, перерегулирование) во многих случаях находятся в противоречии. В частности, увеличение коэффициента усиления разомкнутой уменьшает статическую ошибку, но одновременно снижает запас устойчивости, увеличивает скорость изменения регулируемой величины, что может вызвать сильный колебательный процесс, большое перерегулирование и увеличение времени переходного процесса. Сравнительно легкий выбор передаточных функций, параметров корректирующих устройств, и схем их включения помогает найти решение, удовлетворяющее всем требованиям эксплуатации системы. В частности, для получения астатической системы вводят интегрирующее звено, а для превращения астатической системы в статическую, что бывает необходимо для повышения устойчивости, интегрирующий элемент охватывают жесткой обратной связью – пропорциональным звеном с передаточной функцией W К.У = k. При желании получить быстродействующую систему, не переходя к статической системе, интегрирующий элемент охватывают гибкой обратной связью. Такая система в переходном процессе работает как статическая, а в конце переходного процесса - как астатическая. Следовательно, эта система будет астатической и одновременно, будет иметь большой запас устойчивости и более высокое быстродействие, чем система без обратной связи. Для увеличения быстродействия в некоторых САР на вход усилителя одновременно с сигналом, пропорциональным отклонению D x, подается сигнал, пропорциональный скорости d (D x)/ dt. Введением воздействия по производной позволяетувеличить быстродействие системы в результате того, что в начале процесса на усилитель подается большой сигнал D x S = D x + d (D x)/ dt,
а по мере подхода системы к положению равновесия этот сигнал уменьшается (рис.1.13). Если система начинает отрабатывать сигнал ошибки при его значении, большем чем D при t =t 1,то при введении воздействия по производной отработка начнется при t 2< t 1. Введение сигнала по производной увеличивает быстродействие и запас устойчивости, не влияя на статическую характеристику системы. В САР в качестве корректирующих элементов используются жесткие и гибкие обратные связи, а также введение воздействий по производной и по интегралу. В общем случае в системах регулирования по отклонению выходной сигнал регулятора, подаваемый на вход регулирующего органа, является функцией отклонения D x и времени: u (t) = k п D x + k и ò D xdt + k д(d (D k)/ dt). Эта функция определяет закон регулирования САР. На практике используются различные комбинации сигналов, например: в ПД-регуляторе используются сигналы k п D x и k д(d (D k)/ dt), в ПИ-регуляторе - сигналы k п D x и k и ò D xdt, а в ПИД-регуляторе - все три сигнала. Автоматические регуляторы по характеру действия разделяются на следующие виды: позиционные, статические (пропорциональные), астатические (интегральные), изодромные (пропорционально-интегральные), изодромные с первой производной (пропорционально-интегрально-дифференциальные). При позиционном регулировании регулируемый параметр все время изменяется от минимального до максимального значения. Для позиционного регулирования технологических параметров широко используются автоматические компенсаторы (мосты, потенциометры и др.) со встроенными контактными устройствами, позволяющими осуществлять двух- и трехпозиционное регулирование. Астатическими регуляторами называют такие, у которых при отклонении регулируемого параметра от заданного значения регулирующий орган перемещается в одном направлении. При отклонении регулируемой величины от заданного значения астатический регулятор перемещает регулирующий орган до тех пор, пока не восстановится ее значение до уровня задания. В астатических САР отклонение регулируемой величины от заданного значения в установившемся режиме равно нулю при любой величине внешнего воздействия. Астатические регуляторы имеют большое время переходного процесса, а также может возникнуть перерегулирование в переходном процессе. Статические регуляторы – это такие, у которых перемещение регулирующего органа происходить пропорционально отклонению регулируемого параметра от заданного значения. Статическая САР имеет в установившемся состоянии определенную зависимость между величиной отклонения регулируемого параметра от заданного значения и величиной возмущающего воздействия. В статических САР регулирующее воздействие однозначно связано с отклонением регулируемой величины от заданного значения и всегда имеется статическая ошибка регулирования, зависящая от величины и знака внешнего воздействия. Изодромные регуляторы обладают одновременно свойствами пропорциональных и интегральных регуляторов. Действие регуляторов можно рассматривать как совместное действие статического и астатического регуляторов. Наличие упругой (изодромной) обратной связи, действие которой проявляется в переходном процессе, позволяет повысить качество регулирования. Изодромные регуляторы применяются при регулировании объектов с быстро и резко меняющимися нагрузками и при наличии передаточного запаздывания. Изодромные регуляторы с предварением или ПИД-регуляторы обладают одновременно свойствами статического и астатического регуляторов с дополнительным воздействием по скорости изменения регулируемой величины. В этих регуляторах дополнительно вводится обратная связь по скорости изменения регулируемой величины. Эти регуляторы используются для объектов с большим запаздыванием. В особо ответственных случаях применяются САР, обеспечивающие автоматическую перенастройку регулятора при изменении внешних условий, изменяя значения коэффициентов, составляющих выходного сигнала регулятора k п, k и, k д. Такие системы называются самонастраивающимися или адаптивными. Литература 1. Автоматизация и роботизация строительства: Учеб. пособие / А.Г. Булгаков, В.А. Воробьев, С.И. Евтушенко, Д.Я. Паршин. — М.: РИОР: ИНФРА-М, 2013. — 452 с. 3. Паршин Д.Я. Основы автоматизации и роботизации / РГСУ — Ростов н/Д, 2013. — 147 с.
|

 .
. ,
,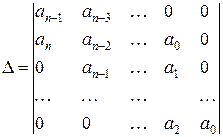
 ;
; 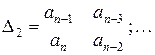
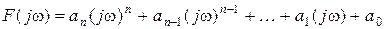
 .Уравнение вектора получается на основе характеристического уравнения системы при подстановки в него p=jw. Разделив вещественную и мнимую части, вектор представляется в виде
.Уравнение вектора получается на основе характеристического уравнения системы при подстановки в него p=jw. Разделив вещественную и мнимую части, вектор представляется в виде .
. В соответствии с этим выражением строится кривая Михайлова в плоскости (X, jY) при различных значениях частоты (рис.1.9). Для устойчивости САР необходимо и достаточно, чтобы вектор F (j w) при изменении w от 0 до
В соответствии с этим выражением строится кривая Михайлова в плоскости (X, jY) при различных значениях частоты (рис.1.9). Для устойчивости САР необходимо и достаточно, чтобы вектор F (j w) при изменении w от 0 до  против часовой стрелки, где n - степень характеристического уравнения системы. Следовательно, для устойчивости САР кривая Михайлова должна последовательно проходить число квадрантов, равное порядку ее дифференциального уравнения.
против часовой стрелки, где n - степень характеристического уравнения системы. Следовательно, для устойчивости САР кривая Михайлова должна последовательно проходить число квадрантов, равное порядку ее дифференциального уравнения.
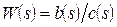 – передаточная функция разомкнутой системы;
– передаточная функция разомкнутой системы;  – характеристический полином замкнутой системы;
– характеристический полином замкнутой системы;  – характеристический полином разомкнутой системы. Положим
– характеристический полином разомкнутой системы. Положим  , тогда
, тогда .
. угол поворота вектора
угол поворота вектора  составляет
составляет  , где
, где  ;
;  ;
;  . В устойчивой системе
. В устойчивой системе  , угол
, угол  определяется из выражения так
определяется из выражения так  , тогда
, тогда  .
. Следовательно, для устойчивой системы вектор
Следовательно, для устойчивой системы вектор  при изменении
при изменении  от 0 до
от 0 до  . Так как функция
. Так как функция  отличается от функции
отличается от функции  при изменении
при изменении  раз точку (–1, j 0).
раз точку (–1, j 0). замкнутой системы нужно, чтобы АФЧХ. разомкнутой системы не охватывала точку (–1, j 0). На рис. 1.11 показан вид годографов
замкнутой системы нужно, чтобы АФЧХ. разомкнутой системы не охватывала точку (–1, j 0). На рис. 1.11 показан вид годографов  Устойчивость САР является необходимым, но недостаточным условием ее практической пригодности. Для технического использования системы необходимо, чтобы они были не только устойчивыми, но и удовлетворяли требованиям качества регулирования. Под качество процесса регулирования понимается способность автоматического регулятора поддерживать с достаточной степенью точности заданный закон изменения регулируемой величины. Качество процесса регулирования оценивается по переходной характеристике y (t) (рис.1.12) с помощью так называемых показателей качества регулирования. Основными из них являются статическая ошибка регулирования, перерегулирование, время регулирования и характер затухания переходного процесса. Статическая ошибка характеризует точность достижения регулируемой величиной своего нового установившегося значения. Она равна абсолютному отклонению регулируемой величины от установившегося значения по окончанию переходного процесса. САР будет удовлетворять предъявляемым к ним требованиям, если статическая ошибка не превышает допустимой величины, задаваемой техническими условиями. Часто статическую ошибку регулирования выражают в процентах к установившемуся значению y уст регулируемой величины
Устойчивость САР является необходимым, но недостаточным условием ее практической пригодности. Для технического использования системы необходимо, чтобы они были не только устойчивыми, но и удовлетворяли требованиям качества регулирования. Под качество процесса регулирования понимается способность автоматического регулятора поддерживать с достаточной степенью точности заданный закон изменения регулируемой величины. Качество процесса регулирования оценивается по переходной характеристике y (t) (рис.1.12) с помощью так называемых показателей качества регулирования. Основными из них являются статическая ошибка регулирования, перерегулирование, время регулирования и характер затухания переходного процесса. Статическая ошибка характеризует точность достижения регулируемой величиной своего нового установившегося значения. Она равна абсолютному отклонению регулируемой величины от установившегося значения по окончанию переходного процесса. САР будет удовлетворять предъявляемым к ним требованиям, если статическая ошибка не превышает допустимой величины, задаваемой техническими условиями. Часто статическую ошибку регулирования выражают в процентах к установившемуся значению y уст регулируемой величины .
. .
.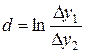 .
.



