Математическое описание САР и их динамические характеристики
Процессы, происходящие в автоматических системах, описываются в установившихся режимах при помощи алгебраических уравнений с постоянными коэффициентами, в неустановившихся режимах – дифференциальными и интегрально-дифференциальными уравнениями. Так как уравнения статического режима можно получить как частный случай уравнений динамики, то остановимся на рассмотрении методов математического описания САР в динамическом режиме. В общем случае неустановившийся процесс в САР может быть описан дифференциальным уравнением вида
где у - регулируемая величина; x - внешнее воздействие. В теории автоматического регулирования получила распространение запись дифференциальных уравнений в алгебраизированной форме. Алгебраизация уравнений позволяет ввести понятие передаточной функции и упростить анализ автоматических систем. При нулевых начальных условиях алгебраизация диференциальных уравнений осуществляется путем формальной замены знака операции дифференцирования символом;
В теории операционного исчисления доказывается правомерность такой замены. Оператор р в этом случав выступает в роли коэффициента, которому можно придавать значения числа и производить над ним любые действия. Дифференциальное уравнение динамики САР в алгебраизированной форме имеет вид
Множитель при х называется оператором воздействия, а множитель при у – собственным оператором. Отношение двух названных операторов
называется передаточной функцией и обозначается W (s). Передаточная функция является математическим выражением динамических свойств элементов. Поведение САР в установившихся и динамических режимах существенно зависит от того, как изменяются во времени внешние воздействия, приложенные к системе. Так как реальные законы изменения внешних воздействий заранее неизвестны, т.е. представляют собой случайные функции времени, то при исследовании САР используют так называемые типовые законы изменения внешних воздействий. Этим воздействиям соответствуют типовые динамические характеристики. В качестве типовых принимают либо наиболее вероятные, либо наиболее неблагоприятные законы изменения задающего и возмущающего воздействий.
Реакция системы на ступенчатое воздействие x (t)=1(t) называется переходной функцией h (t). Она может быть определена экспериментально или в результате решения дифференциального уравнения системы. Частотные характеристики изображают реакцию системы на синусоидальное изменение входной величины. Регулируемая величина при этом будет изменяться также по закону синуса и с той же частотой, но с другой амплитудой и фазой. Другими словами, если
где х о и у о – амплитуды колебаний входного и выходного сигналов; w – круговая частота колебаний; t – время; j – запаздывание в передаче сигнала. Поскольку при х о = const, у o и j зависят не только от частоты изменения входного сигнала, но и от динамических свойств системы, то отношение этих величин
представляет собой частотную характеристику системы, которая называется амплитудно-фазовой частотной характеристикой (АФЧХ) и имеет общий вид
Функция А (w) называется амплитудной частотной характеристикой, а функция j(w) фазовой частотной характеристикой. Исследование САР значительно упрощаются, если использовать логарифмические частотные характеристики (ЛЧХ). При построении логарифмической амплитудно-частотной характеристики (ЛАЧХ) по оси абсцисс откладывается частота в логарифмическом масштабе, а по оси ординат выходная амплитуда в децибелах, равная Для математического описания динамики САР и анализа её работы систему удобно рассматривать не в виде совокупности отдельных связанных между собой элементов автоматики, а разбивать на динамические звенья. Под элементарным динамическим звеном понимается искусственно выделяемая часть автоматической системы, которая характеризуется определенными динамическими свойствами и описывается дифференциальным уравнением не выше второго порядка.
|

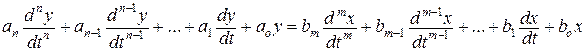 ,
,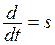 . При этом справедливы равенства
. При этом справедливы равенства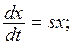
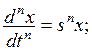
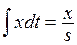 и т.д.
и т.д.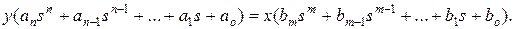

 Для оценки динамических свойств САР применяются также переходные и частотные характеристики, которые изображают реакцию системы на ступенчатое (кривая 1) и гармоническое (кривая 2) типовые воздействия (рис.1.7). Переходные характеристики изображают изменение во времени выходной величины, когда входная величина изменяется скачком от 0 до 1 и затем остается постоянной. Ступенчатое воздействие описывается уравнением единичной функции
Для оценки динамических свойств САР применяются также переходные и частотные характеристики, которые изображают реакцию системы на ступенчатое (кривая 1) и гармоническое (кривая 2) типовые воздействия (рис.1.7). Переходные характеристики изображают изменение во времени выходной величины, когда входная величина изменяется скачком от 0 до 1 и затем остается постоянной. Ступенчатое воздействие описывается уравнением единичной функции
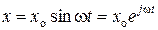 , то
, то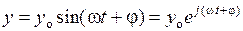 ,
,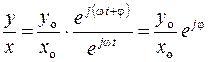
 .
. . При построении логарифмической фазовой частотной характеристики (ЛФЧХ) масштаб по оси абсцисс остается логарифмическим, а значения фазы по оси ординат откладывается в градусах или радианах.
. При построении логарифмической фазовой частотной характеристики (ЛФЧХ) масштаб по оси абсцисс остается логарифмическим, а значения фазы по оси ординат откладывается в градусах или радианах.


