И элементов автоматических устройств
При управлении технологическими процессами объектами является технологическое оборудование или процесс производства материальной продукции. Целенаправленное управление технологическое оборудование по заданным техническим и технико-экономическим критериям обеспечивается системой управления технологическим процессом. Построение таких систем в первую очередь определяется свойствами объектов управления. Различают объекты управления непрерывного и дискретного действия. В объектах непрерывного действия можно выделить параметры, которые поддерживаются на заданном уровне или изменяются по определенному закону. В этом случае между входными и выходными величинами всех элементов существует непрерывная функциональная связь. В общем виде такие объекты характеризуются рядом параметров, представляющих его обобщенные координаты: – управляемые величины – управляющие воздействия – возмущающие воздействия Эти параметры можно рассматривать как компоненты соответствующих векторов:
Решением задачи управления является определение вектора управляющего воздействия Зависимость вектора управляющего воздействия от векторов управляемых величин, возмущающих воздействий и времени называется алгоритмом управления:
Регулирование рассматривается как частный случай управления. При регулировании по отклонению алгоритм управления представляется функцией ошибки управления
Объекты дискретного действия, выполняют ряд рабочих операций, которые циклически повторяющиеся в определенной последовательности. При автоматическом управлении такими объектами управляющие устройства осуществляют заданную логическую последовательность включения и отключения исполнительных механизмов. Поэтому такие системы называют автоматическими системами логико-программного управления. В качестве математического описания таких систем составляются уравнения алгебры логики и выполняются их преобразования на основе законов Булевой алгебры. Преобразования выполняются в соответствии с выбранной элементной базой. Автоматическая система создается для управления определенным объектом, поэтому, прежде чем автоматизировать объект, необходимо хорошо изучить его характеристики. Может оказаться, что объект не поддается автоматизации или, наоборот, без автоматического регулятора он вообще работать не может. Свойства объекта управления выражаются следующими основными характеристиками: емкостью, временем разгона, самовыравниванием. Значение регулируемой величины объекта управления зависит от поступления вещества или энергии, которое определяется разностью притока Q np и расхода Q p (D Q = Q пр – Q ст). При D Q = 0 значение регулируемой величины остается постоянным во времени и такое состояние называется равновесным. Изменение регулируемой величины происходит вследствие управляющих воздействий, влияющих на расход или приток. Возмущающим воздействием может быть изменение нагрузки, связанное с режимом работы объекта, или помехи, т. е. внешние воздействия не связанными с нормальной работой объекта. Например, в баке с водой регулируемой величиной является уровень воды, нагрузкой - расход воды, регулирующим воздействием - подача воды, а помехами - утечки. Многие объекты управления, например баки, обладают способностью накапливать энергию или вещество. Эта способность называется емкостью объекта и определяет скорость изменения регулируемой величины при изменении разности между притоком и расходом. Если эта скорость линейно зависит от разности притока и расхода d x вых / d t = D Q / C, то величина С называется коэффициентом емкости. Численно он равен количеству энергии или материи, воздействия которых изменяют регулируемую величину на единицу в течение 1 с. В безразмерной форме последние уравнение можно записать в виде
T p = C (x вых. н / D Q max); x вых. н - номинальное значение регулируемой величины. Величина Т рназывается временем разгона,а обратная ей величина n=1/ T р - чувствительностью объекта к возмущению,или скоростью разгона. В зависимости от времени разгона Т и коэффициента передачи К различают следующие объекты: безынерционные, неуправляемые, статические объекты с самовыравниванием, объекты без самовыравнивания, неустойчивые объекты.
Безынерционные объектыописываются линейным уравнением x вых = Kq при Т» 0. При регулировании этих объектов необходимо обеспечить высокое быстродействие регулятора. В неуправляемых объектах регулируемая величина остается постоянной при изменении q: dx вых / d t» 0 при T»¥. Примером таких объектов являются баки, если для регулирования уровня жидкости в них использованы краны с малым проходным сечением. Статические объекты после приложения возмущения D q переходят без регулятора из одного равновесного состояния в другое (рис.1.5, а). Примером таких объектов являются сушильные и пропарочные камеры, обжиговые печи, регулируемая величина у которых - температура, бак со свободным расходом жидкости. Объекты без самовыравнивания описываются дифференциальным уравнением вид а T p = d x вых / d t =D q, при r = 0 (К = ¥). Регулируемая величина их неограниченно возрастает с постоянной скоростью 1/ T p (рис.1.5, б). Примером таких объектов являются конвейерные линии и лифты, если за регулируемую величину принимается их перемещение, баки и бункера для хранения жидких и сыпучих материалов, регулируемая величина у которых - количество материала или его уровень в баке. В неустойчивых объектах при r < 0 (К < 0) регулируемый параметр увеличивается с возрастающей скоростью (рис.1.5, в) x вых = K (e- t/T - 1).Примером такого объекта может служить монтируемая строительная деталь, например панель, если она опирается на малую поверхность, а центр тяжести ее находится выше поверхности опоры. Каждый элемент системы характеризуется функцией преобразования, которая представляет собой зависимость выходного сигнала от входног. Особенности этого преобразования определяются статической и динамической характеристиками элемента. Статической характеристикой элемента называется зависимость выходного сигнала от входного в установившемся режиме. Если характеристика линейна, то аналитическая связь x вых с x вх записывается в виде x вых = k x вх, где k - коэффициент усиления. Элемент, имеющий такую характеристику, называется линейным. Тангенс угла наклона характеристики равен коэффициенту усиления. Если зависимость нелинейная, то она обычно представляется графически.
Динамической характеристикой элемента называется изменение выходной величины во времени x вых(t). Эта характеристика отражает инерционность элемента, его динамические свойства. Динамику линейного элемента описывают линейным дифференциальным уравнением, в котором переменные величины x вых и x вх представляются в безразмерной форме:
где x выхо и x вхо - постоянные значения физических величин, соответствующие установившемуся режиму. В большинстве случаев в качестве динамической характеристики элементов удобно рассматривать переходную функцию, которая представляет собой решение дифференциального уравнения элемента при скачкообразном изменении входной величины.
|

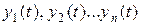 ;
; ;
; .
.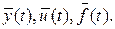 В любой момент времени состояние управляемой системы является функцией начального состояния управляемой величины
В любой момент времени состояние управляемой системы является функцией начального состояния управляемой величины  и векторов
и векторов 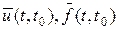 , то есть
, то есть
 обеспечивающего функционирование системы.
обеспечивающего функционирование системы.
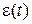 и времени t:
и времени t:


 где xвых = x вых / xвых . н; D q = (Q пр – Q ст) / D Q max = D Q / D Q max;
где xвых = x вых / xвых . н; D q = (Q пр – Q ст) / D Q max = D Q / D Q max;
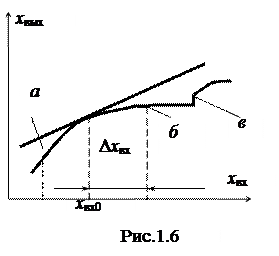 Анализ систем, содержащих нелинейные элементы, является трудной задачей, поэтому стремятся нелинейную характеристику заменить приближенной линейной, исходя из того, что во многих случаях элемент работает при небольших изменениях входного сигнала относительно среднего значения x вх0. В этом случае приближенная линейная зависимость определяется касательной к кривой x вых(x вх), проведенной в точке xвхо (рис.1.6). Замена нелинейной характеристики линейной на участке а-б называется линеаризацией. Она возможна в тех случаях, когда нелинейная характеристика не имеет разрывов и скачков. Ошибка линеаризации тем меньше, чем меньше отклонение входной величины x вх от значения x вх0, при котором производилась линеаризация.
Анализ систем, содержащих нелинейные элементы, является трудной задачей, поэтому стремятся нелинейную характеристику заменить приближенной линейной, исходя из того, что во многих случаях элемент работает при небольших изменениях входного сигнала относительно среднего значения x вх0. В этом случае приближенная линейная зависимость определяется касательной к кривой x вых(x вх), проведенной в точке xвхо (рис.1.6). Замена нелинейной характеристики линейной на участке а-б называется линеаризацией. Она возможна в тех случаях, когда нелинейная характеристика не имеет разрывов и скачков. Ошибка линеаризации тем меньше, чем меньше отклонение входной величины x вх от значения x вх0, при котором производилась линеаризация. ;
; 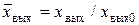 ,
,


