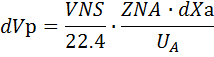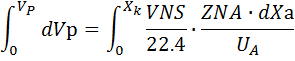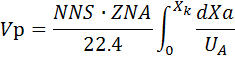Модель идеального вытеснения.
Xa Xa + dXa Выделяем элементарный объем dL. На левой границе степень превращения ключевого компонента состоит Xа, а на правой XаdXа Элементарный объем не перемещается относительно корпуса реактора. В течении элементарного промежутка времени в границах элементарного объема можно пренебречь неравномерным распределением вещества. В границах элементарного объема отсутствует диффузионный перенос вещества. Соответственно в уравнении материального баланса отсутствует слагаемое, характеризующее диффузионный перенос. Количество вещества А, которое подошло к левой границе элементарного объема NNS Количество компонента А, которое прореагировало будет равно произведению скорости: = NNS
Для газов:
Интегрируем
Уравнение материального баланса реактора рассчитывается по модели идеального вытеснения. Анализ этого уравнения показывает, что на величину объема реактора, необходимого для достижения заданной степени превращения, оказывается, влияют следующие параметры: 1)Расход реакционной смеси 2)Концентрация ключевого компонента 3)Температура 4)Давление Очевидно, что при увеличении расхода реакционной смеси для достижения заданной степени превращения ключевого компонента, необходимо увеличить объем реактора. Для обратимой эндотермической реакции скорость процесса с увеличением температуры возрастает, поэтому объем реактора, необходимый для достижения заданной производительности с увеличением температуры уменьшается. Для обратимой экзотермической реакции зависимость скорости от температуры проходит через максимум, соответственно зависимость объема реактора, необходимого для достижения заданной производительности от температуры будет проходить через минимум. Для любого необратимого процесса все аналогично эндотермической реакции.
|





 dL
dL


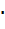 ZNA
ZNA