В случае малого числа измерений доверительный интервал среднего значения
Е = хср – Х можно найти по формуле Стьюдента Е= ts×s, где ts – коэффициент Стьюдента, который находится по таблице.
Табл. Значение ts для различных значений доверительной вероятнотси Рs и числа измерений n.
| n Ps
| 0,5
| 0,6
| 0,7
| 0,8
| 0,9
| 0,95
| 0,98
| 0,99
| 0,999
| |
|
0,816
0,765
0,741
0,727
0,718
0,711
0,706
0,703
0,7
0,697
0,692
0,688
| 1,376
1,061
0,978
0,941
0,92
0,906
0,896
0,889
0,883
0,879
0,876
0,868
0,861
| 1,963
1,336
1,25
1,19
1,156
1,134
1,119
1,108
1,11
1,093
1,088
1,076
1,066
| 3,08
1,886
1,638
1,533
1,476
1,44
1,415
1,397
1,383
1,372
1,363
1,345
1,328
| 6,31
2,92
2,35
2,13
2,02
1,943
1,895
1,86
1,833
1,812
1,796
1,761
1,729
| 12,71
4,3
3,18
2,77
2,57
2,45
2,36
2,31
2,26
2,23
2,2
2,14
2,09
| 31,8
6,96
4,54
3,75
3,36
3,14
2,9
2,82
2,76
2,72
2,62
2,54
| 63,7
9,92
5,84
4,6
4,03
4,71
3,5
3,36
3,25
3,17
3,11
2,98
2,86
| 636,6
31,6
12,94
8,61
6,86
5,96
5,4
5,04
4,78
4,59
4,49
4,14
3,88
|
Оценка погрешности производится в соответствии с видом измерения физической величины. Измерения бывают прямые и косвенные, однократные и многократные, прямые и косвенные.
Правила, используемые при оценке погрешностей косвенных измерений:
- при сложении и вычитании абсолютные погрешности складываются;
- при умножении и делении относительные погрешности складываются;
- при возведении в степень и извлечении корня относительные погрешности умножаются на показатель степени;
- дисперсия суммы и разности величин равна сумме их дисперсий.
Причем, погрешность результата измерения всегда значительно меньше самого результата.
Средняя квадратичная погрешность функции z(a,b,…) многих переменных:
 . Аналогично, для абсолютных погрешностей. . Аналогично, для абсолютных погрешностей.
Алгоритм обработки результатов многократных измерений.
1. Найти среднее арифметическое значение хср измеряемой величины: 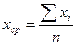 . .
2. Найти абсолютные погрешности отдельных измерений:  . .
3. Определяем среднюю квадратичную погрешность среднего значения:  . .
4. По числу наблюдений n и выбранной вероятности Р по таблице определяем коэффициент Стьюдента ts.
5. Вычисляем доверительный интервал для среднего значения измеряемой величины: Е= ts×s.
6. Записываем результат измерений в виде: Х= хср ± Е (Р=Рs).
7. Определяем относительную погрешность измерений в процентах: e= 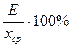 . .
В случае однократных прямых измерений с помощью измерительного прибора погрешность зависит от класса точности прибора К. К – число, равное предельно допустимой погрешности, выраженной в процентах от верхнего предела измерения прибора. Т.о.  , где с - цена деления прибора, Nm – наибольшее число делений в приборе. Погрешность от текущего измерения: D х =0,01× К × х, где х – показание прибора. Доверительная вероятность этих приборных измерений равна 1. , где с - цена деления прибора, Nm – наибольшее число делений в приборе. Погрешность от текущего измерения: D х =0,01× К × х, где х – показание прибора. Доверительная вероятность этих приборных измерений равна 1.
В случае многократных прямых измерений доверительная погрешность, соответствующая доверительной вероятности Р находится по формуле: 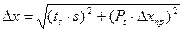 . .
Обработка результатов косвенных измерений:
1) выполнить прямые однократные или многократные измерения и найти средние значения аргументов; вычислить абсолютные погрешности каждого аргумента;
2) для аргументов определенных путем однократных измерений вычислить доверительные погрешности с заданной доверительной вероятностью D хi=Рt×Dxпр;
3) для аргументов, найденных при многократных измерениях, определить средние квадратичные погрешности и по методу Стьюдента их абсолютные погрешности с нужной доверительной вероятностью;
4) найти абсолютную погрешность функции данных аргументов по формуле: 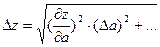 . .
5) среднее значение функции z: zср=z(aср, bср, …);
6) если функция удобна для логарифмирования, то т.к. 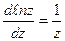 , находим относительную погрешность: , находим относительную погрешность: 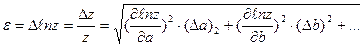 ; ;
7) абсолютная погрешность находится как произведение относительной погрешности на значение самой величины;
8) окончательный результат записывается в виде: z = zср ± Dz (P=Pz).

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
Правила наложения мягкой бинтовой повязки 1. Во время наложения повязки больному (раненому) следует придать удобное положение: он должен удобно сидеть или лежать...
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
|
Измерение следующих дефектов: ползун, выщербина, неравномерный прокат, равномерный прокат, кольцевая выработка, откол обода колеса, тонкий гребень, протёртость средней части оси
Величину проката определяют с помощью вертикального движка 2 сухаря 3 шаблона 1 по кругу катания...
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
|
|

 . Аналогично, для абсолютных погрешностей.
. Аналогично, для абсолютных погрешностей.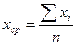 .
. .
. .
.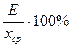 .
. , где с - цена деления прибора, Nm – наибольшее число делений в приборе. Погрешность от текущего измерения: D х =0,01× К × х, где х – показание прибора. Доверительная вероятность этих приборных измерений равна 1.
, где с - цена деления прибора, Nm – наибольшее число делений в приборе. Погрешность от текущего измерения: D х =0,01× К × х, где х – показание прибора. Доверительная вероятность этих приборных измерений равна 1.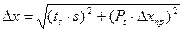 .
.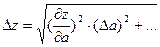 .
.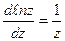 , находим относительную погрешность:
, находим относительную погрешность: 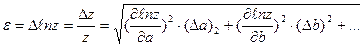 ;
;


