Ход работы.
Вычисления погрешности округления. Практическая работа 1. Цели: научиться определять абсолютную и относительную погрешности числа; научиться определять верные значащие цифры числа; научиться определять погрешности функций Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения Порядок выполнения работы. 1. Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже). 2. Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы. Теоретический материал Понятие погрешности числа Разность точного и приближенного значений величины называется погрешностью приближения ( обозначается т.е. откуда х= а + т.е. истинное значение равно сумме приближенного значения и погрешности приближения. Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближенного значения числа х. т.е. Запись х= а Пример 1. На предприятии 1284рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 -1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 - 1280 = 4.
Пример 2. Даны приближенные значения числа х= Решение: Находим Пример 3. Длина детали х (см) заключена в границах 33 Решение: Примем за приближенное значение длины детали среднее арифметическое границ: а=(33+34)/2 = 33,5 (см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину 33,5-0,5 х=33,5 Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается Т.е.
Пример 1. При измерении длины L и диаметра проводника получили L =(10,0 Решение: Измерение длины проводника производилось с точностью до 0,1м=100мм, а измерение диаметра проводника – с точностью до 0,1мм. При измерении длины проводника допускается абсолютная погрешность в 100мм на 10000мм, и, следовательно, допустимая абсолютная погрешность составляет
При измерении диаметра допустимая абсолютная погрешность составляет
Пример 2. Известно, что 0,111 является приближенным значением для Решение:Здесь х=
Пример 3. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна
|

 х),
х), х=х- а - погрешность приближения
х=х- а - погрешность приближения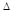 х,
х,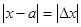 - абсолютная погрешность приближения.
- абсолютная погрешность приближения.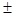 h означает, что истинное значение величины х заключено между границами, т.е. а - h
h означает, что истинное значение величины х заключено между границами, т.е. а - h 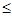 х
х  ;
; 

 Какое из этих трех приближений является лучшим?
Какое из этих трех приближений является лучшим?
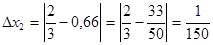 ;
; 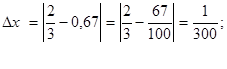 Лучшим приближением числа х является
Лучшим приближением числа х является 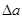 можно найти и как полуразность верхней и нижней границ, т.е.
можно найти и как полуразность верхней и нижней границ, т.е. 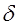 .
.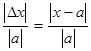 =
=  измеряемой величины.
измеряемой величины.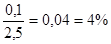 измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.
измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.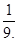 Найти абсолютную и относительную погрешности этого приближения.
Найти абсолютную и относительную погрешности этого приближения.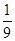 , а =0,111. Тогда
, а =0,111. Тогда 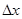 = х- а = 1/9 – 0,111 = 1/9000-а.п.п,
= х- а = 1/9 – 0,111 = 1/9000-а.п.п,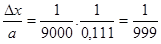 -о.п.п
-о.п.п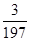 или, округленно,
или, округленно, 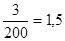 %.
%.


