Частотный критерий Михайлова.
Введем в характеристическое уравнение частотный параметр путем замены р = jco, где со - круговая частота. Тогда уравнение примет вид комплексного: D(jω) = - jA0·ω3 – A1·ω2 + jA2·ω + A3; т. e. D(jω) = P(ω)+jQ(ω), где P(ω) = Аз – A1·ω2 (вещественная составляющая); jQ(ω) = j(A2·ω - А0·ω3) (мнимая составляющая). Подставим значения коэффициентов А0 – А3 и, меняя значения круговой частоты, получим ряд комплексных чисел, которые сведем в табл.1.
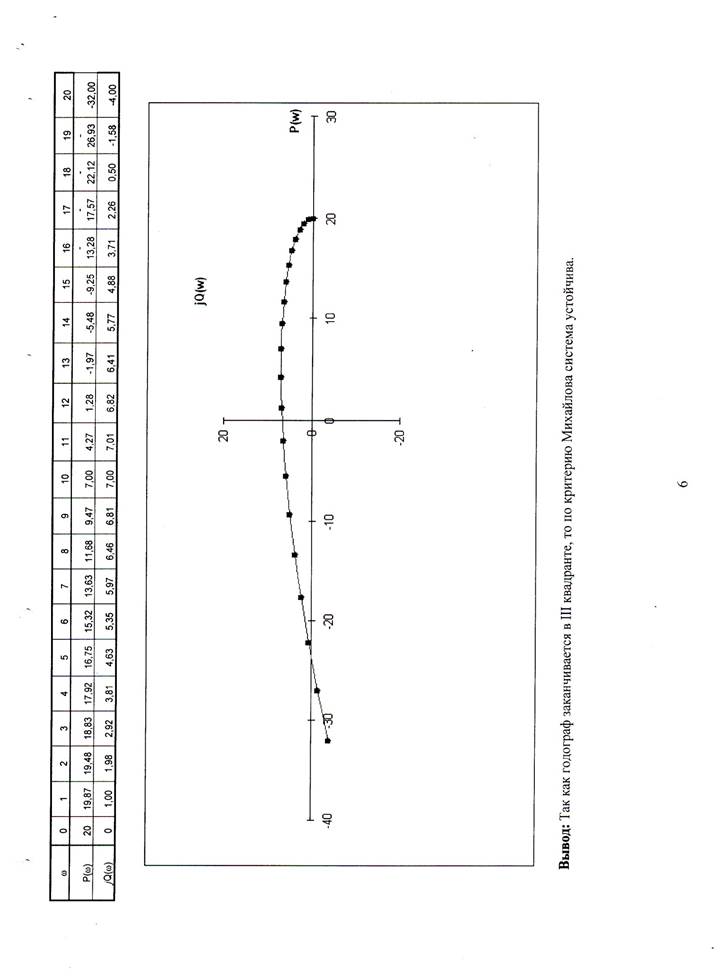
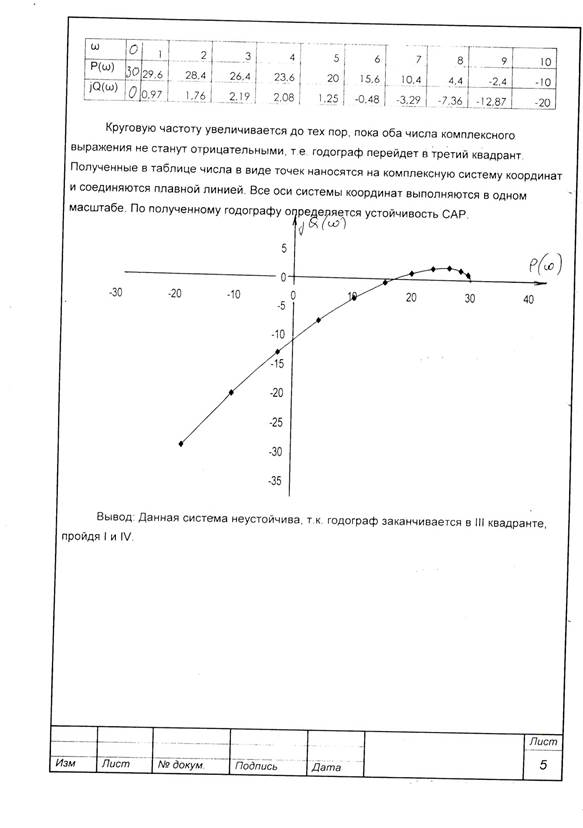
Круговую частоту увеличивать до тех пор, пока оба числа комплексного выражения станут отрицательными, т.е. годограф перейдет в третий квадрант. Полученные в таблице числа в виде точек нанести на комплексную систему координат и соединить плавной линией. Все оси системы координат выполняются в одном масштабе. По полученному годографу определить устойчивость системы автоматического регулирования. По критерию Михайлова система третьего порядка будет устойчива, если годограф заканчивается в 3 квадранте, пройдя через 1 и 2, и неустойчива в любом другом случае. Вывод: данная система устойчива (неустойчива), т.к. годограф... Пример заполнения таблицы 1 и нанесения годографа на систему координат приведены дальше.
|