Теоретико – вероятностный подход к обработке неопределенностей(плохо определенной информации) Pi = (Ci→Ri, Ki) Ei→Hi Ei – свидетельство Hi – гипотеза Pi (Hiǀ Ei) P = (E→H) P(HǀE) Формула Байеса P = (HǀE) = P (EǀH) Модификация
Поделим
Pi+=P(Ei Pi-= P(Ei =
БЗ
Пример: <Грипп, P, 2, {(1: 0,99; 0,01); (2: 0,9; 0,1)}> 1. Нет эпидемии P=0,01 a) E1(↑t) P(HǀE1)= b) E2(Насморк) P(HǀE2)= c) E1, E2 P(Hǀ E1,E2) 2. Эпидемия P=0,1 a) P(HǀE1)=0,9 b) P(HǀE2)=0,5 c) P(Hǀ E1,E2)=1
|
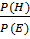
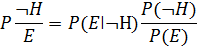
- шанс справедливости гипотезы H
- Условный шанс
– Модифицированная формула Байеса
– E-контр свидетельство
– E-свидетельство
, если свидетельства 
независимы
, i=1,n
, j=1,m
) 
P=P(H) P (HǀEi) = P(EiǀH) 
H) P(Ei) = P(Ei 
H)*P(H)+P(Ei 
– Априорная вероятность
– Свидетельство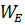
– Номер свидетельства
