Метод субъективных коэффициентов уверенности.
P(HǀE1…En)=0,6 P(˥HǀE1…En)=0,4 Мера доверия Мd(HǀE) Мера недоверия Mn(HǀE)
Max
K(HǀE) = Md(HǀE)-Mn(HǀE) – коэффициент уверенности 0 -1 Kпорог, н Если свидетельства сложные, то Ei и Ej независимы.
Mn(Hǀ Ei)+Mn(Hǀ Ej)- Mn(Hǀ Ei)*Mn(Hǀ Ej)
Mn((HǀEi)+Mn(HǀEj)- Mn(HǀEi)*Mn(HǀEj) Md(Ht&HgǀE) = min Mn(Ht&HgǀE) = max Md(Ht Mn(Ht Если свидетельства правдоподобные Md(HǀA) = Md(HǀE)*max Mn(HǀA) = Mn(HǀE)*max
|

 Md(HǀE)= 1, если P(H) = 1
Md(HǀE)= 1, если P(H) = 1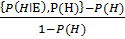 , если P(H)
, если P(H) 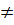 1
1 Mn(HǀE)= 1, если P(h)=0
Mn(HǀE)= 1, если P(h)=0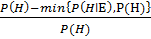 , если P(H)
, если P(H) 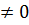
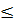 Md, Mn
Md, Mn  (1)Md(HǀEi&Ej) = 0, если Md(Hǀ Ei&Ej)=1
(1)Md(HǀEi&Ej) = 0, если Md(Hǀ Ei&Ej)=1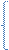 (2)Mn(HǀEi&Ej)= 0, если Md(HǀEi&Ej)=1
(2)Mn(HǀEi&Ej)= 0, если Md(HǀEi&Ej)=1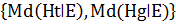
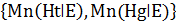
 HgǀE) = max
HgǀE) = max 



