Метод покоординатного спуска
Идея всех методов спуска состоит в том, чтобы из начального приближения точки x(0)=(x1(0), x2(0),…, xn(0)) перейти в точку x(1)=(x1(1), x2(1),…, xn(1)) такую, чтобы f(x(0))> f(x(1)). Пусть в области D задано нулевое приближение x(0). Фиксируем значение x2(0),x3(0),…, xn(0) и рассматриваем функцию f(x1, x2(0),…, xn(0)) как функцию одной переменной x1. Находим минимум этой функции Далее фиксируем значения x3(0),x4(0),…, xn(0) и рассматриваем функцию f(x1(1), x2,x3(0),…, xn(0)) как функцию одной переменной x2 и т.д. После n шагов получим f(x1(1), x2(1),x3(1),…, xn(1))≤ f(x1(0), x2(0),x3(0),…, xn(0)). В результате первого шага покоординатного спуска происходит переход из начальной точки x0 в точку x1. 1) если f(x(0))= f(x(1)), то x(0) – точка минимума f(x). 2) если f(x(0))> f(x(1)), то выполняется следующий шаг покоординатного спуска, в котором за начальную точку принимается x(1). Этот процесс продолжается до тех пор, пока f(x(k+1))-f(x(k))<ε, где ε – заданная точность.
|
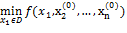. Пусть x1(1) доставляет минимум этой функции. f(x1(1), x2(0),…, xn(0))≤ f(x1(0), x2(0),…, xn(0)).
