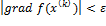Метод градиентного спуска
Численные методы отыскания минимума состоят в построении последовательности векторов {x(k)}, удовлетворяющих условию f(x(0))> f(x(1))>…> f(x(k)). В этих методах элементы последовательности вычисляются по формуле x(k+1)=x(k)+hk* Как известно, градиент функции в некоторой тоске направлен в сторону наискорейшего локального возрастания функции, следовательно, спускаться нужно в направлении, противоположному градиенту. Этот вектор называется антиградиентом. Используя антиградиент в качестве направления спуска, приходим к итерационному процессу вида:
Все методы спуска, в которых вектор Для минимизации функции используется метод градиентного спуска с дроблением шага. Процесс (1) с дроблением шага протекает следующим образом: выбираем некоторое значение x(0), затем выбираем hk=h=const и на каждом шаге процесса выбираем условие монотонности f(x(k+1))<f(x(k)). Если это условие нарушается, то h дробим до тех пор, пока монотонность не восстановится. Для окончания счета можно использовать критерии:
Наиболее важным моментом в этом методе - это выбор шага. Формула (1) с постоянным шагом практически не применяется.
|
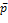(k), где 
(1)
