Метод Симпсона

Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).

 

9. Простейшие формулы численного интегрирования.

Квадратурная формула левых прямоугольников

Очевидно, что ее алгебраическая степень точности d=0 и формула является интерполяционной.

Квадратурная формула правых прямоугольников

Квадратурная формула средних прямоугольников

Алгебраическая степень точности d=1 и формула является интерполяционной.

Квадратурная формула трапеций

Квадратурная формула Симпсона

10. Обобщение простейших формул численного интегрирования.

?

11. Задача Коши для обыкновенного дифференциального уравнения 1-го порядка.

Задача Коши для обыкновенного дифференциального уравнения состоит в том, чтобы найти решение уравнения y' = f(x, y) (2), удовлетворяющее начальным условиям

y(x₀) = y_0. (3)

Решение задачи Коши называется частным решением уравнения (2) при условии(3). Частному решению соответствует одна из интегральных кривых, проходящих через точку (x₀,y₀).

Будем искать приближенное решение этой задачи на конечном множестве точек отрезка [a, b], называемом сеткой:

x_i = x₀ + ih, x₀ = a, x_n = b,

h = (b-a)/n, i = 0,1,2,...,n.

Приближенным решением задачи будет некоторая сеточная функция y = y (x).

Для получения значений сеточной функции используются различные методы основанные на замене производной каким-либо разностным уравнением.

12. Метод Эйлера решения задачи Коши для ОДУ 1-го порядка.

Простейшим численным методом решения задачи Коши является метод ломанных Эйлера. Суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=x_i. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:

13. Одномерные задачи оптимизации.

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. Если рассматривать функцию, то поиск наибольшего или наименьшего значения. Общие методы оптимизации:

1. аналитические методы, использующие классические методы дифференциального и вариационного вычисления

2. численные методы

3. графические методы

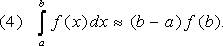
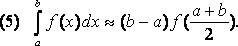
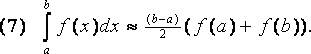
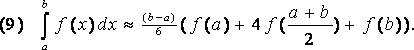
Функция f(x), заданная на a≤x≤b называется унимодальной на отрезке [a,b], если существует единственная точка x^* минимума f(x), т.е. f(x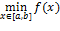^*)= и если для любых двух точек x₁, x₂ 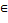[a,b] выполняются условия: f(x₁)>f(x₂), что следует из неравенства x₁<x₂≤x^* и f(x₁)<f(x₂), что следует из неравенств x₂>x₁≥x^*.