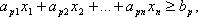Метод наискорейшего спуска. Вычисление градиента на каждом шаге, позволяющее всё время двигаться в направлении наиболее быстрого убывания функцииВычисление градиента на каждом шаге, позволяющее всё время двигаться в направлении наиболее быстрого убывания функции, в то же время может замедлить вычислительный процесс. Часто пользуются модификацией градиентного метода, получившее название метод наискорейшего спуска. Согласно этому методу после вычисления в начальной точке градиента функции делают в направлении антиградиента не маленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют процедуру. Таким образом, в методе наискорейшего спуска величина hk определяется из условия:
т.е. на каждом шаге решается задача минимизации. 15. Задачи линейного программирования. Задачи оптимизации, в которых целевая функция представлена в виде линейной комбинации, а ограничения в виде линейных неравенств, называются задачами линейного программирования. Задачи линейного программирования заключаются в нахождении таких значений
Среди ограничений часто встречаются условия неотрицательности всех или части переменных:
|
,
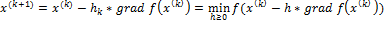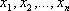, которые максимизируют или минимизируют линейную функцию 
в условиях ограничений:
