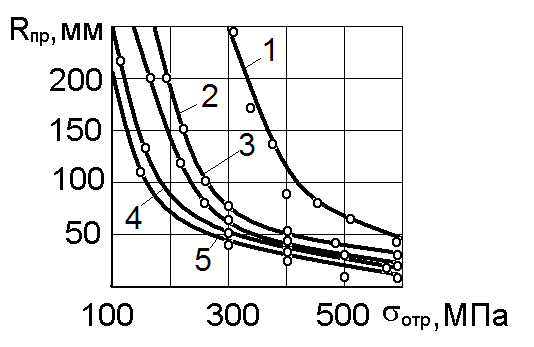
Изгиб призматических образцов с различной шириной b и соотношением толщин слоев h Tiили h Ст, вырезанных из сваренного взрывом титано-стального биметалла ВТ1-0 + 08Х18Н10Т, осуществляли вокруг цилиндрической оправки различного радиуса при жестком защемлении одного из концов. На длину зоны изгиба L, входящей в выражение (2.3), практически не влияли толщины слоев h Ti или h Ст и механические свойств СКМ, но она линейно зависела от ширины изгибаемого образца b (рис.2.3). Наблюдается хорошая сходимость экспериментальных значений R пр с расчетными как для узких (кривые 1 и 2), так и для широких (кривые 4 и 5) образцов с различной исходной прочностью σотр соединения BT1-0 - 08Х18Н10Т (рис. 2.4). Предельный радиус кривизны R пр образцов с высокой прочностью соединения σотр (кривые 3 и 4, рис. 2.4) значительно меньше, чем для образцов с низкой исходной прочностью (кривая 1, рис. 2.4). Как видно из рис. 2.4 и 2.5, зависимости R пр = f (σотр) и R пр = f (b) имеют гиперболический характер.
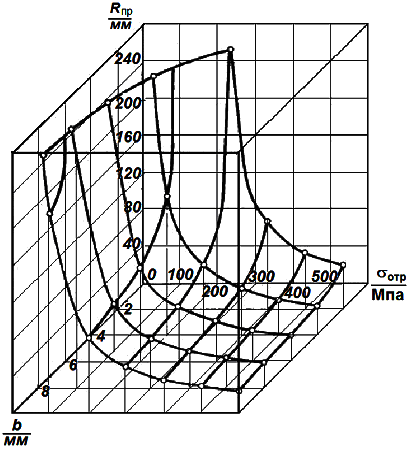
Обобщенная трехмерная диаграмма, связывающая величину R пр с исходной прочностью σотр и шириной b титано-стальных полос при h 1 = h 2 = 5 мм, представлена на графике (рис. 2.6).

| Рис.2.3. Зависимость длины зоны изгиба L от ширины b биметаллической полосы
|
Установлено, что уменьшение толщины как одного из слоев СКМ при постоянной толщине другого, так и одновременно обоих слоев приводит к повышению деформационной способности биметалла. Наибольшей деформационной способностью обладают полосы с соотношением h Ti/ h Ст>1, при хорошей сходимости расчетных по выражению (2.10) и экспериментальных значений R пр, поскольку модуль текучести Е Т1 титана BT1-0 значительно ниже Е Т2 стали 08X18H10T.
| 
|
| Рис. 2.4. Зависимость предельного радиуса изгиба R пр от исходной прочности σотр биметаллической полосы BT1-0+08X18H10T: 1 – b = 2 мм; 2 – b = 4 мм; 3 – b = 6 мм; 4 – b = 8 мм; 5 – b = 10 мм
| Рис. 2.5. Зависимость предельного радиуса изгиба Rпр от ширины b биметаллической полосы BT1-0+08X18H10T: 1 – σотр = 300 МПа; 2 – σотр = 400 МПа; 3 – σотр = 500 МПа; 4 – σотр = 600 МПа
|
На графике рис. 2.7 представлена расчетно-экспериментальная зависимость R пр для биметаллической полосы шириной b = 2 мм с исходной прочностью σотр = 500 МПа от суммарной толщины h Ti + h Ст, где кривая 1 соответствует h Ti / h Ст <1, кривая 2 – равенству толщин титанового и стального слоев, кривая 3 – соотношению h Ti / h Ст >1.
| 
|
| Рис. 2.6. Зависимость предельного радиуса изгиба R пр от исходной прочности σотр и ширины b биметаллической полосы
| Рис. 2.7. Зависимость R пр биметаллической полосы от h Ti+ h Ст : 1− h Ст = 5 мм; 2− h Ti = h Ст; 3− h Ti = 5 мм
|
Испытания на отрыв слоев биметаллических образцов с исходной прочностью σотр = 420 – 570 МПа показали, что изгиб практически не снижает исходную прочность биметалла как в области больших, так и малых радиусов кривизны деформаций. На графике (рис. 2.8) представлена экспериментальная зависимость прочности на отрыв от радиуса изгиба. Увеличение радиуса изгиба свыше предельного практически не влияет на прочность на отрыв композита титан ВТ1-0 - 08Х18Н10Т.

| Рис. 2.8. Зависимость прочности σотр биметалла ВТ1-0 + 08Х18Н10Т от радиуса изгиба
|









