Теоретическая часть. Помимо равнопрочности паяных соединений при одноосном растяжении, необходимо обеспечить равнопрочность паяного шва М кольцевой формы основным материалам ОМ и
Помимо равнопрочности паяных соединений при одноосном растяжении, необходимо обеспечить равнопрочность паяного шва М кольцевой формы основным материалам ОМ и при действии внутреннего давления Р в в соответствии со схемой (рис.5.1). Давление на наружную поверхность вставки большего диаметра приводит к «заклиниванию» высверленного канала в биметалле и несущая работоспособность сварно-паяного узла будет определяться, в основном, механическими свойствами материалов вставки и композиционного соединения. Расчет прочности комбинированного узла из разнородных материалов проводится с учетом основных положений теории контактного упрочнения со следующими допущениями: пластически деформируется только мягкая прослойка (паяный шов) и прилегающие к ней участки более прочных материалов вставки и биметалла; металлы комбинированного узла являются упруго-пластичными; для учета деформационного упрочнения диаграммы деформирования металлов аппроксимируются на уровне значений изгиб узла отсутствует.
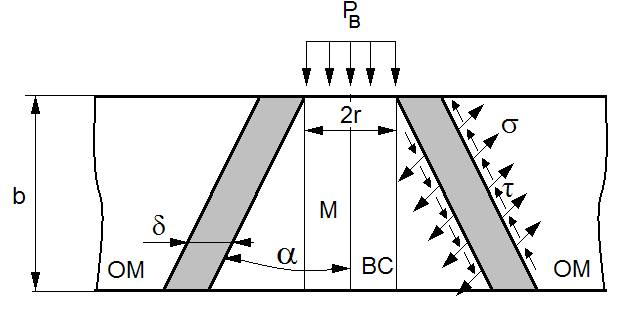
Рис. 5.1. Схема разнородного соединения конусной вставки (ВС) со стенкой пластины (оболочки) Исследуемое разнородное соединение представляет собой соединение с мягкой прослойкой, наклоненной под углом α к оси симметрии конусной вставки (рис.5.2). Рассматриваемая задача сводится к определению предельного состояния тонкого пластического слоя (М), заключенного между более прочными участками вставки (ВС) и основного металла (ОМ), при одновременном действии сдвигающих (τ) и растягивающих (σ) напряжений. При этом τ и σ связаны с внешним давлением Р в, действующим на конусную вставку (ВС), следующим образом:
где Предельное состояние наклонной прослойки при одновременном действии на нее сдвигающих и растягивающих сил можно оценить из соотношения
где τпр и σпр − предельные значения τ и σ при нагружении рассматриваемых соединений на сдвиг или растяжение. Средние предельные напряжения σпр, определяющие несущую способность мягкой прослойки при статическом растяжении, можно найти из соотношения
где Согласно (5.4) при изменении относительной толщины прослойки χ в пределах
С учетом (5.1) − (5.3) соотношение для оценки несущей способности соединения конусной вставки с пластиной (или оболочкой)
Рис. 4.2. Зависимость оптимальной относительной толщины мягкой прослойки χоп от угла ее наклона и степени механической неоднородности Для практических инженерных расчетов предельного давления, действующего на конусную вставку, предложена номограмма (рис.5.3) с помощью которой по известным значениям α, x,
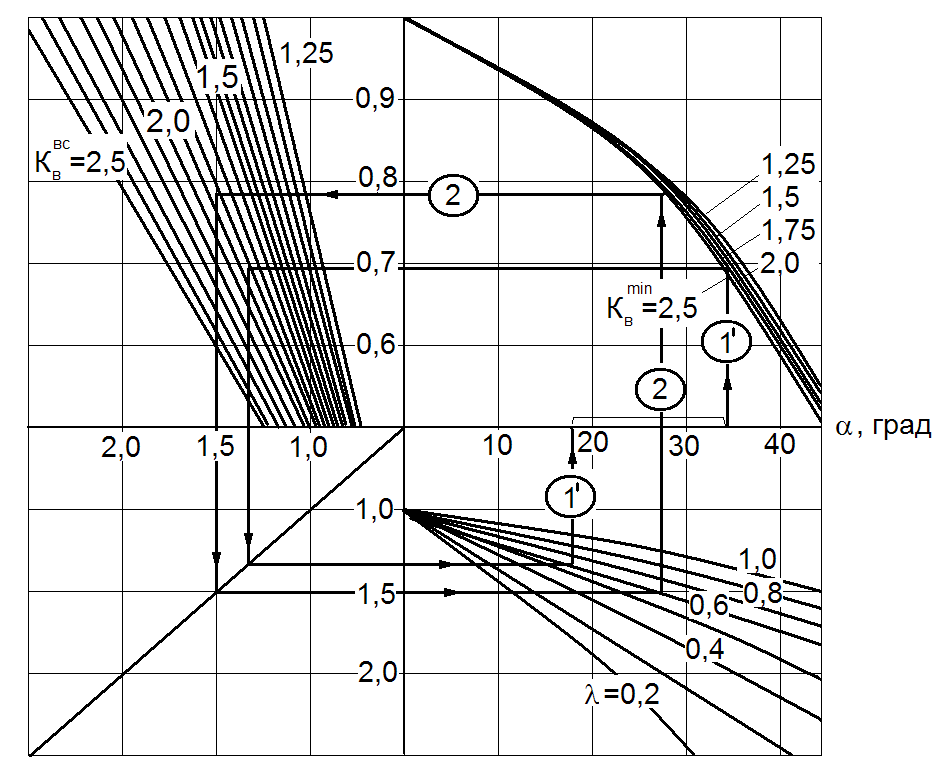
Рис. 5.3. Номограмма для определения величины предельного давления рв, действующего на конусную вставку Выражение (5.8) может быть преобразовано в номограмму (рисунок 5.4), позволяющую по известным значениям
Рис. 5.4. Номограмма для определения оптимальных значений углов наклона конусной вставки αon в разнородных соединениях
|

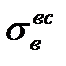 ,
, 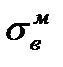 и
и 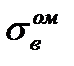 ;
;
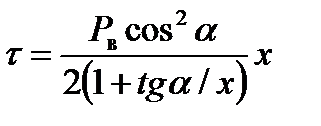 (5.1)
(5.1) (5.2)
(5.2)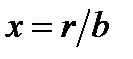 − относительный радиус конусной вставки.
− относительный радиус конусной вставки. , (5.3)
, (5.3)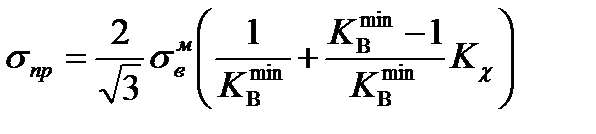 (5.4)
(5.4) − степень механической неоднородности соединений минимальная из
− степень механической неоднородности соединений минимальная из 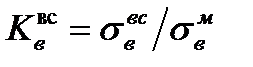 и
и  ;
; 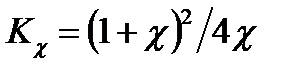 − коэффициент контактного упрочнения мягкой прослойки при растяжении нормально к контактной поверхности.
− коэффициент контактного упрочнения мягкой прослойки при растяжении нормально к контактной поверхности. (рис.4.2) величина
(рис.4.2) величина 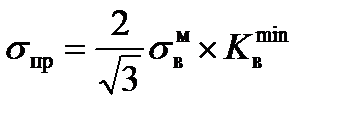 , то есть имеет место равнопрочность соединения менее прочному из основного металла или металлу вставки. Предельное значение сдвигающих напряжений τпр равно пределу текучести при чистом сдвиге металла прослойки
, то есть имеет место равнопрочность соединения менее прочному из основного металла или металлу вставки. Предельное значение сдвигающих напряжений τпр равно пределу текучести при чистом сдвиге металла прослойки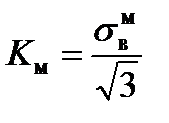 (5.5)
(5.5)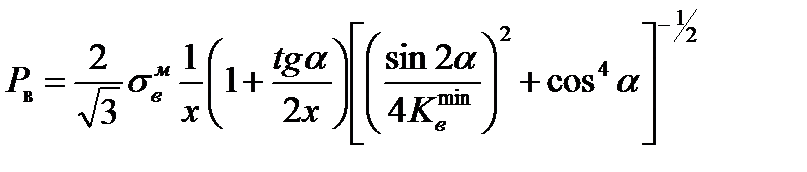 (5.6)
(5.6) (5.7)
(5.7)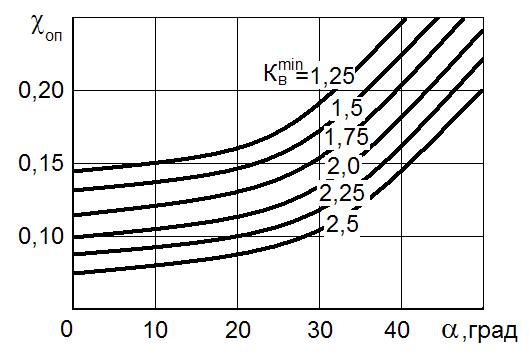
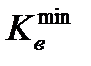
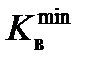 определяется величина Pв. При заданном сочетании параметров α, x, χ,
определяется величина Pв. При заданном сочетании параметров α, x, χ, 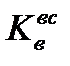 может быть обеспечена равнопрочность рассматриваемого соединения металлу конусной вставки. В этом случае возможен перенос разрушения с прослойки на конусную вставку, которая срезается по цилиндрической поверхности диаметром 2 r, показанной на рис.5.2 тонкими линиями. Равнопрочность рассматриваемых соединений материалу конусной вставки описывается следующим выражением:
может быть обеспечена равнопрочность рассматриваемого соединения металлу конусной вставки. В этом случае возможен перенос разрушения с прослойки на конусную вставку, которая срезается по цилиндрической поверхности диаметром 2 r, показанной на рис.5.2 тонкими линиями. Равнопрочность рассматриваемых соединений материалу конусной вставки описывается следующим выражением: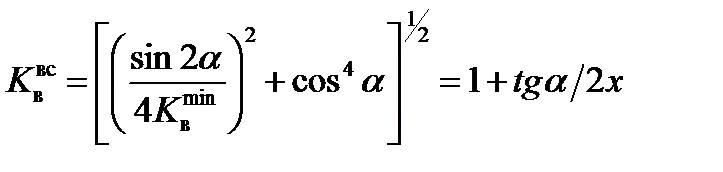 (5.8)
(5.8)
 ,
, 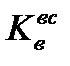 и x определять оптимальное значение угла наклона образующей конусной вставки αоп, при котором обеспечивается равнопрочность соединения материалу вставки. Определение αon осуществляется методом последовательных приближений. После определения αon по соотношению (5.7) с учетом
и x определять оптимальное значение угла наклона образующей конусной вставки αоп, при котором обеспечивается равнопрочность соединения материалу вставки. Определение αon осуществляется методом последовательных приближений. После определения αon по соотношению (5.7) с учетом 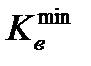 находят величину χоп.
находят величину χоп.