Решение. В соответствии с определениями для десятичных знаков приближенного числа в «узком» и «широком» смыслах заключаем
В соответствии с определениями для десятичных знаков приближенного числа в «узком» и «широком» смыслах заключаем, что поскольку у числа a четыре верные цифры в широком (узком) смысле, то абсолютная погрешность данного числа не превосходит единицы (половины единицы) последнего верного разряда, т.е. имеем: a = 338.1 2 D(шс) = D D(ус) = D В случае, если приближённое число a имеет четыре (т.е. не меньше трёх верных знаков в узком смысле - n = 4), то практически справедлива формула:
В нашем случае:
В случае, если приближённое число a имеет четыре (т.е. не меньше трёх верных знаков в широком смысле - n = 4), то справедлива формула:
В нашем случае:
|

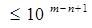 Þ D
Þ D 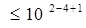 Þ D (шс) ≤ 0.1;
Þ D (шс) ≤ 0.1;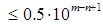 Þ D
Þ D 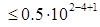 Þ D (ус) ≤ 0.05.
Þ D (ус) ≤ 0.05.
 .
.
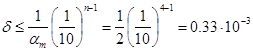 = 0.00033 ≈ 0.0 3%.
= 0.00033 ≈ 0.0 3%.


