Решение. Для вычисления значения функции (1) «точные» иррациональные числа:
Для вычисления значения функции (1) «точные» иррациональные числа:
необходимо заменить «приближенными» (округленными) значениями:
Поэтому считаем, что в формулу, определяющую значения функции (y), входят три приближённых аргумента и данную функцию следует рассматривать как функцию вида:
Запишем далее значения данных приближённых чисел (аргументов) с четырьмя верными знаками:
Следовательно, (в узком смысле) абсолютная погрешность каждого из чисел (аргументов функции y) одинакова и равна: D
Вычислим (на инженерном калькуляторе) для D
Для абсолютной погрешности D y результата вычисления функции y приближённых значений аргументов
или:
где:
Поскольку в данном случае:
то, следовательно
Поскольку приближённое значение функции y = 0.538624 имеет абсолютную погрешность Dy = 0.0004, то количество его n верных (в узком смысле) десятичных знаков, может быть определено из неравенства:
в нашем случае имеем неравенство вида:
которое, очевидно, выполняется при n £ 3. Следовательно, полученное значение функции y = 0.538624 необходимо округлить до трёх верных значащих цифр:
Итак, полученный результат:
имеет абсолютную погрешность
|


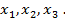


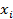 (ус) = D
(ус) = D 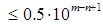
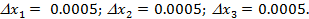
 (ус) приближённое значение функции c большим количеством запасных значащих цифр:
(ус) приближённое значение функции c большим количеством запасных значащих цифр:



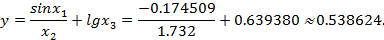
 имеем:
имеем:














 и три верных знака:
и три верных знака:



