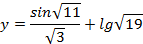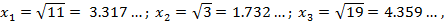Решение. Из известного подхода к решению обратной задачи теории погрешности в рамках принципа равных абсолютных погрешностей
Из известного подхода к решению обратной задачи теории погрешности в рамках принципа равных абсолютных погрешностей, погрешность (и количество верных знаков у приближенных значений аргументов) определяется из соотношения:
на основе e - требуемого значения погрешности результата вычисления функции:
поэтому из условия задачи необходимо выяснить каково заданное значение погрешности e - результата вычисления функции:
при условии, что этот результат должен быть вычислен с четырьмя верными знаками. Заметим, что старший десятичный разряд m результата вычисления функции
при любом количестве верных десятичных знаков у приближённых аргументов
функция
будет иметь значение y» 0.672613, а при наличии у приближенных аргументов четырех верных десятичных знаков (см. задание №6) y» 0.539. Следовательно, из соотношения:
и из требования вычислить функцию:
с четырьмя верными знаками (n = 4) следует, что погрешность e, с которой нужно вычислить значение данной функции определяется неравенством:
Далее решаем обратную задачу теории погрешностей в рамках предположения о равенстве абсолютных погрешностей аргументов, на основе соотношения:
При этом для сокращения объёма вычислений значения величин:
целесообразно взять из Задания №6:
Поэтому, находим:
Следовательно, заключаем, что значения погрешностей приближенных аргументов должны удовлетворять неравенству:
Далее зная, что погрешности
необходимо определить какое количество верных десятичных знаков следует сохранить при использовании этих аргументов, т.е. чисел:
Поскольку в данном случае наши аргументы имеют значения:
то при их десятичной записи по формуле: xi = am 10 m + am- 110 m- 1 + am- 210 m- 2 + am- 310 m- 3 + … + am- n +110 m- n +1 + …; значение старшего десятичного разряда m = -1, следовательно, в данном случае при наличии у аргументов
следует взять (не менее чем) с пятью верными знаками (n = 5), потому что в этом случае абсолютная погрешность аргументов (в узком смысле) не будет превышать величины
Для того чтобы вычисленное значение функции:
имело четыре верных знака в узком смысле, приближённые значения аргументов:
следует округлить до пяти верных десятичных знаков.
|

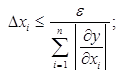 i = 1, 2, …, n или
i = 1, 2, …, n или 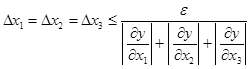 ,
,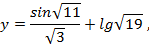
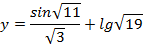
 равен -1, т.е. m = -1. Действительно, даже при округлении значений приближённых аргументов только до одного верного десятичного знака:
равен -1, т.е. m = -1. Действительно, даже при округлении значений приближённых аргументов только до одного верного десятичного знака:
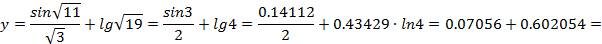
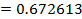

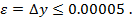
 .
.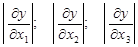
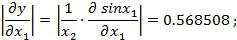




 приближённых аргументов
приближённых аргументов 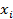 должны удовлетворять неравенству:
должны удовлетворять неравенству: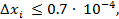


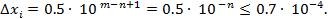
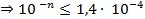 .
.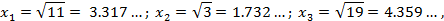
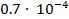 :
: