Решение. а) При округлении числа = 3.316624790355399 до n – верных десятичных знаков (в узком/широком смысле)
а) При округлении числа D a £ 0.5×10 m- n +1; D a £ 10 m- n +1. Поэтому согласно условию задачи необходимо потребовать, чтобы: D a £ 0.5×10 m- n +1 £ 0.007; D a £ 10 m- n +1 £ 0.007. Поскольку при записи числа a» 0.5×10 - n +1 = 5×10 - n £ 0.007; 10 - n +1 £ 0.007. Откуда следует, что n соответственно должно удовлетворять неравенствам: n ³ 3 и n ³ 4. Следовательно, для того чтобы при округлении числа б)Поскольку для числа a цифра a m = 3, то
|
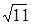= 3.316624790355399… до n – верных десятичных знаков (в узком/широком смысле), абсолютная погрешность D a полученного приближенного числа a будет соответственно удовлетворять соотношениям:
абсолютная погрешность полученного приближенного числа a =3.31662… (в узком/широком смысле) не превышала 0.007 необходимо взять соответственно не менее трёх/четырех верных десятичных знаков.
отсюда 10 n - 1 ³ 33,333… и Þ n ³ 3.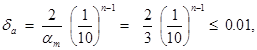
отсюда 10 n - 1 ³ 66,667… и Þ n ³ 3. 
