З А Д А Н И Я
по молекулярной физике Составили: к. ф.-м. н. доцент Замураев В.П., к. ф.-м. н. доцент Калинина А.П. Замечание. После каждой задачи в скобках указаны номера задач, которые должны быть решены на семинарах перед сдачей данной задачи. В скобках после номера задачи указан номер соответствующего семинара. Номера задач соответствуют учебно-методическому пособию:
1. Замураев В.П., Калинина А.П. Задачи по термодинамике и молекулярной физике. Новосибирск: Изд. НГУ, 2003.
Задание 1 (молекулярная физика)
1. Пользуясь табличными значениями и асимптотическим (х >> 1) представлением интеграла erf(x) = 1 – 1/(p1/2 x) × exp(– x 2), рассчитать: а) долю частиц, у которых | vx | ³ vm; б) долю частиц, у которых v ³ vm; в) долю частиц в атмосфере Земли, скорость которых превосходит вторую космическую v 2 = 11,2 км/с. T = 300 К, m = 29. (№ 2.10, 2.12 (2)) 2. Пленки некоторых нерастворимых органических кислот и спиртов можно моделировать идеальным двумерным газом. Считая, что такой идеальный газ находится в неравновесном состоянии, в котором все молекулы имеют одинаковые по модулю скорости v и изотропно распределены по направлениям движения в плоскости пленки, найти распределение для проекций скоростей на некоторую ось в плоскости пленки. С его помощью рассчитать давление газа и число ударов молекул о единичный отрезок границы пленки. Концентрация газа n, масса молекулы m. (№ 2.15, 2.16 (3)) 3. В эксперименте с молекулярным пучком ртути получена следующая зависимость числа частиц Δ N, попавших на экран за постоянное время t >> v м/с = 150 200 250 300 350 400 450 500 550 600 650 700. Δ N · 10-9 = 61 195 415 664 856 915 835 663 417 287 155 70. Построить график распределения молекул ртути по скоростям в печке. Какова приблизительно температура паров ртути в печке? В процессе измерений ω; = const, l = const. Обратите внимание на то, что интервал скоростей молекул, проходящих
через вертушку, не остается постоянным. (№ 2.18 (3), 2.25 (5)) 4. Из сосуда объемом V газ истекает в вакуум через малые отверстия общей площадью S. Как во времени нужно подводить тепло к газу, чтобы его температура оставалась неизменной? Как будет изменяться температура газа в адиабатически изолированном сосуде? Начальная плотность газа n 0. (№ 2.18 (3), 3.24, 3.29 (15)) 5. Два полых цилиндра с поперечными сечениями S и 2 S и одинаковой высоты h соединены встык и образуют замкнутый сосуд. В его объем закачан идеальный газ при температуре T. Найти относительное изменение давления в нижней части сосуда при его переворачивании, возникающее при учете неравномерности распределения газа по высоте. Оценить его для условий Земли. (№ 2.38, 2.43 (7)) 6. В центрифуге радиуса R, вращающейся с угловой скоростью ω;, находится смесь двух газов с молекулярными весами μ;1 и μ;2 и количеством молекул N 1 и N 2. Найти отношение плотностей газов у внешней стенки и на оси центрифуги. Сделать оценки для смесей H 2 ¾ D 2 и U235 ¾ U238; R =10 см, ω = 104 (№ 2.44 (8)) 7. Рассчитать распределение по скоростям точечных частиц после упругого столкновения с бесконечно тяжелой сферой. До столкновения все частицы имеют одинаковую скорость v. (№ 3.3, 3.4 (11)) 8. Молекулы реального газа взаимодействуют друг с другом по закону u = – а / r 6 при r > d, где d – эффективный диаметр молекулы. Найти зависимость сечения соударений s от температуры (поправка Сезерленда), считая соударением соприкосновение частиц. (№ 3.3, 3.4 (11)) 9. Оценить время испарения воды из трубки длиной 10 см, запаянной с одного конца. Температура комнатная. Первоначально вода заполняла трубку наполовину. Относительная влажность воздуха 50 %, давление насыщенных паров 27 мм рт. ст. Длина свободного пробега молекул в системе воздух–пар порядка 10–5 см. Пар у поверхности воды считать насыщенным, капиллярными явлениями пренебречь. (№3.8, 3.9 (13)) 10. Определить, на какой угол φ; повернется диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см вращается второй такой же диск с угловой скоростью ω; = 50 с – 1. Радиус дисков R = 10 см, модуль кручения нити f = 100 дин · см / рад. Между дисками находится аргон (газокинетический диаметр атома 3,6 (№3.21 (14), 3.35 (16)) 11. Для измерения теплопроводности газа им заполняется пространство между двумя длинными коаксиальными цилиндрами радиуса r 1 и r 2. Заполнение производится при невысоком давлении (~ 10 мм рт. ст.), чтобы исключить конвекцию. Внутренний цилиндр нагревается источником тепла с удельной мощностью Q, установившиеся температуры цилиндров t 1 и t 2 измеряются. Рассчитать коэффициент теплопроводности и газокинетический диаметр молекулы для азота, если r 1 = 0,5 см, r 2 = 2 см, Q = 0,038 вт / см, t 1 = 93 (№ 3.13, 3.15 (14)) 12. В сферическом реакторе радиуса R, заполненном газообразной смесью реагентов, идет химическая реакция. Тепловой эффект реакции в расчете на единичный объем равен Q. Какой поток тепла следует снимать с поверхности реактора, если ее температура поддерживается равной T 0? Найти распределение температуры в реакторе. Учесть зависимость коэффициента теплопроводности от температуры. (№ 3.15, 3.16 (14))
Задание 2 (термодинамика)
1. Из сосуда, в котором находится газ при комнатной температуре и под давлением (№ 1.8, 1.14 (19)) 2. Идеальный газ сжимается под поршнем в цилиндре так, что уходящее в окружающую среду тепло равно изменению внутренней энергии газа. Определить работу, затраченную на сжатие моля газа при изменении объема в два раза. Чему равна теплоемкость в этом процессе? Начальная температура газа T 0. (№ 1.14 (19)) 3. Один моль H2O с температурой 25 (№ 1.29, 1.30 (22)) 4. Идея динамического отопления, высказанная В. Томсоном (1852 г.), заключается в следующем. Тепловой двигатель, в топке которого сжигается уголь, приводит в действие холодильную машину. Холодильная машина отнимает теплоту от природного резервуара воды (например, от грунтовой воды) и отдает ее воде в отопительной системе. Одновременно вода в отопительной системе служит холодильником теплового двигателя. Определить теоретическое количество тепла, которое получает отапливаемое помещение от сжигания 1 кг каменного угля. Удельная теплота сгорания угля q = 8000 ккал / кг, температура в котле паровой машины t 1 = 210 (№ 1.35 (23)) 5. Найти работу, совершаемую произвольным рабочим телом за цикл, состоящий из адиабаты, политропы и изотермы. (№ 1.43 (24)) 6. Теплоизолированный цилиндрический сосуд разделен поршнем пренебрежимо малой массы на две равные части. По одну сторону поршня находится идеальный газ с массой (№ 1.44 (24)) 7. Выразить изменение температуры свободно расширяющегося одноатомного газа через начальный и конечный объемы и константы уравнения Ван-дер-Ваальса для газа. Оценить изменение энтропии и энтальпии. (№ 1.44 (24), 1.62 (29)) 8. Серебряная проволока диаметром d = 1 мм адиабатически нагружается при комнатной температуре силой F = 10 Н. Полагая, что удельная теплоемкость c = 234 Дж /(К × кг), плотность r = 10 г / см 3, а температурный коэффициент линейного расширения a = 1,9 ×10–5 К –1, определить изменение температуры проволоки. Коэффициент линейного теплового расширения показывает относительное изменение длины тела при нагревании на температуру ΔT при постоянной нагрузке. Работа по растяжению проволоки определяется выражением: dA’= Fdl, где dl – бесконечно малое удлинение проволоки. (№ 1.48 (26), предварительный разбор подхода к решению) 9. Определить точку кипения воды на вершине холма высотой 300 м над уровнем моря. Изменением температуры с высотой пренебречь. Удельная теплота парообразования при нормальных условиях равна 540 кал / г, пар подчиняется уравнению состояния идеального газа. (№ 2.38 (7), 1.103(29)) 10. Теплота плавления льда при 0 (№ 1.103, 1.106 (29)) 11. Капля жидкости находится в равновесии с паром при давлении P 1, которое из–за поверхностного натяжения в капле больше давления P 2 насыщенного пара над плоской поверхностью при той же температуре. Найти критический (равновесный) радиус капли в предположении | P 1 – P 2| ‹‹ P 2. Известны T – температура системы, s – коэффициент поверхностного натяжения, m – молярная масса вещества, r – плотность жидкости. Пар считать идеальным газом и пренебречь молярным объемом жидкости по сравнению с молярным объемом пара. (№ 1.101(28), 1.113 (30), предварительный разбор подхода к решению) 12. Определить, какое количество энергии освобождается при слиянии мелких водяных капель радиусом 2×10-3 мм в одну большую каплю радиусом 2 мм. Насколько при этом повышается температура воды? (№ 1.121 (31))
|

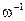 , от скорости (определяемой как v = ω l /α):
, от скорости (определяемой как v = ω l /α):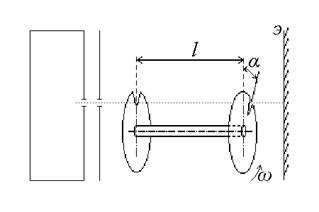
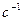 .
.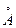 ). Рассмотреть случаи различных давлений и построить график зависимости угла поворота φ; от давления P.
). Рассмотреть случаи различных давлений и построить график зависимости угла поворота φ; от давления P.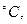 t 2 = 0
t 2 = 0 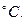
 ,большим атмосферного
,большим атмосферного 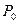 , приоткрыв кран, выпускают газ, пока избыток давления не исчезнет. Затем кран закрывают и, после того как температура в сосуде вновь станет комнатной, измеряют давление в сосуде
, приоткрыв кран, выпускают газ, пока избыток давления не исчезнет. Затем кран закрывают и, после того как температура в сосуде вновь станет комнатной, измеряют давление в сосуде 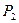 . Как по этим данным найти показатель адиабаты газа γ;? Тот же вопрос для случая, когда в сосуде вначале был воздух под давлением
. Как по этим данным найти показатель адиабаты газа γ;? Тот же вопрос для случая, когда в сосуде вначале был воздух под давлением 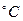 охлаждается до 0
охлаждается до 0 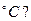 Теплота испарения при 100
Теплота испарения при 100 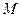 , молекулярным весом μ; и молярными теплоемкостями
, молекулярным весом μ; и молярными теплоемкостями 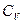 и
и  , не зависящими от температуры, а по другую сторону поршня создан высокий вакуум. Начальная температура и давление газа T 0 и P 0. Поршень отпускают, и он, свободно двигаясь, дает возможность газу заполнить весь объем цилиндра. После этого, постепенно увеличивая давление на поршень, медленно доводят объем газа до первоначальной величины. Найти изменение внутренней энергии и энтропии газа при таком процессе.
, не зависящими от температуры, а по другую сторону поршня создан высокий вакуум. Начальная температура и давление газа T 0 и P 0. Поршень отпускают, и он, свободно двигаясь, дает возможность газу заполнить весь объем цилиндра. После этого, постепенно увеличивая давление на поршень, медленно доводят объем газа до первоначальной величины. Найти изменение внутренней энергии и энтропии газа при таком процессе.


