Дисперсионный анализ
Лабораторная работа № 6 Тема: Применение дисперсионного анализа при обработке информации. Дисперсионный анализ
Одна из задач статистики связана с сопоставлением параметров распределения выборок, т.е. с определением существенных различий в значениях параметров однотипных выборок. Наиболее широкое распространение получил дисперсионный анализ. В дисперсионном анализе исследуются методы проверки гипотезы о равенстве математических ожиданий случайных величин, представленных выборками ограниченного объема. Непосредственное сравнение оценок математических ожиданий совокупности выборок оказывается менее эффективным, чем сопоставление оценок дисперсий, это обстоятельство и дало наименование методу. Подобные задачи возникают при исследовании влияния каких-либо параметров на показатели качества объекта, например: привела ли модернизация оборудования к снижению времени обработки запросов; влияет ли размер кэша второго уровня на производительность системы при решении конкретных задач обработки данных. Эти задачи решаются в рамках однофакторного дисперсионного анализа. В более сложных ситуациях исследуется влияние нескольких факторов на нескольких уровнях (многофакторный дисперсионный анализ). Далее будет рассмотрен только однофакторный анализ. Однофакторный дисперсионный анализ позволяет установить, оказывает ли существенное влияние некоторый фактор Ф на исследуемую случайную величину. Задача сравнения выборок случайных величин формулируется следующим образом. Имеются результаты наблюдений в виде совокупности групп наблюдений, задан уровень значимости α для проверки статистической гипотезы. В данном случае отдельные группы трактуются как выборки одной и той же случайной величины, полученные по результатам наблюдения за одним объектом при различных значениях фактора Ф (количество уровней фактора равно m). Требуется проверить нулевую гипотезу Н 0 о равенстве математических ожиданий случайных величин всех выборок. Иначе говоря, требуется установить, значимо или незначимо различаются выборочные средние значения, вычисленные для каждого слоя. Допущения: генеральные совокупности, соответствующие каждому слою, распределены нормально; дисперсии слоев одинаковы; математические ожидания, дисперсии, законы распределения случайных величин для различных слоев неизвестны, сами случайные величины являются непрерывными. Вполне понятно, что первые два условия являются наиболее существенными и весьма ограничивают область применения методов дисперсионного анализа. Основная идея дисперсионного анализа состоит не в сопоставлении математических ожиданий случайных величин, а в сравнении оценки "факторной дисперсии", порождаемой воздействием фактора, и оценки "остаточной дисперсии", обусловленной случайными причинами. Если различие между этими оценками значимо, то фактор оказывает существенное влияние на случайную величину, в противном случае влияние фактора несущественно. Если установлено существенное влияние фактора, то каждой группе соответствует своя оценка математического ожидания. Упорядочение значений оценок математического ожидания позволит выявить влияние фактора. Пример 1. Три различные группы из шести испытуемых получили списки из десяти слов. Первой группе слова предъявлялись с низкой скоростью -1 слово в 5 секунд, второй группе со средней скоростью - 1 слово в 2 секунды, и третьей группе с большой скоростью - 1 слово в секунду. Было предсказано, что показатели воспроизведения будут зависеть от скорости предъявления слов. Доказать это предположение. Результаты представлены в табл. 1. Таблица 1. Количество воспроизведенных слов (по J. Greene, M D'Olivera, 1989, p. 99)
Известно, что данные подчиняются нормальному закону распределения. Выдвинем нулевую гипотезу: различия в объеме воспроизведения слов между группами являются случайными и не зависят от скорости предъявления слов. Альтернативная гипотеза: Различия в объеме воспроизведения слов между группами являются не случайными и зависят от скорости предъявления слов. Последовательность операций в однофакторном дисперсионном анализе для несвязанных выборок: 1. подсчитаем SSфакт - вариативность признака, обусловленную действием исследуемого фактора. Часто встречающееся обозначение SS - сокращение от "суммы квадратов" (sum of squares).
где Тс – сумма индивидуальных значений по каждому из условий. Для нашего примера 43, 37, 24 (см. табл. 1); с – количество условий (градаций) фактора (=3); n – количество испытуемых в каждой группе (=6); N – общее количество индивидуальных значений (=18);
Отметим разницу между По формуле (1) рассчитав фактическую вариативность признака, получаем:
2. подсчитаем SSобщ – общую вариативность признака:
3. подсчитаем случайную (остаточную) величину SSсл, обусловленную неучтенными факторами:
4. число степеней свободы равно:
5. «средний квадрат» или математическое ожидание суммы квадратов,усредненная величина соответствующих сумм квадратов SS равна:
6. значение статистики критерия Fэмп (критерий Фишера) рассчитаем по формуле:
Для нашего примера имеем: Fэмп=15,72/2,11=7,45 7. определим Fкрит по статистическим таблицам. Для df1=k1=2 и df2=k2=15 табличное значение статистики равно 3,68 8. если Fэмп<; Fкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная гипотеза. Для нашего примера Fэмп > Fкрит (7.45>3.68), следовательно принимается альтернативная гипотеза. Вывод: различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы (Р-значение меньше уровня значимости альфа<0,05, следовательно критерий Фишера значим). Т.о. скорость предъявления слов влияет на объем их воспроизведения.
Решим задачу в Excel. На лист Excel ввести исследуемые данные. Дальше выбираем команду Сервис – Пакет анализа – Однофакторный дисперсионный анализ. В диалоговом окне Входной интервал вводим исходных данных, в разделе Группировка переключатель По столбцам (т.к. результаты по группам расположены в столбцах). Далее указать Выходной диапазон (любую свободную ячейку на листе). Результат анализа. В результате будет получена следующая таблица.
Параметр Альфа определяет статистический уровень значимости для теста (=0,05). SS - вариативность признака, обусловленного действием исследуемого фактора. Df –число степеней свободы MS – «средний квадрат» или математическое ожидание суммы квадратов F – статистика критерия эмпирическая (т.е расчетная) F критическое – определяется по статистическим таблицам Р-значение сравнивается с уровнем значимости. Если P-значение меньше 0,05, критерий Фишира значим, иначе, незначим. если Fэмп<; Fкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная гипотеза Мы получили все те же данные при помощи Excel, вывод такой же.
|

 , (1)
, (1)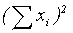 - квадрат общей суммы индивидуальных значений (=1042=10816)
- квадрат общей суммы индивидуальных значений (=1042=10816)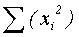 , в которой все индивидуальные значения сначала возводятся в квадрат, а потом суммируются, и
, в которой все индивидуальные значения сначала возводятся в квадрат, а потом суммируются, и 
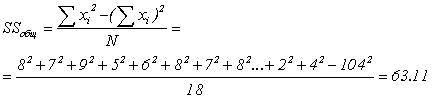 (2)
(2) (3)
(3) =3-1=2 (4)
=3-1=2 (4)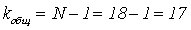

 (5)
(5)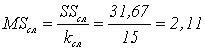
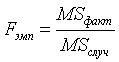 (6)
(6)



