Подставив полученные значения в систему уравнений, получим
Умножив все члены первого уравнения на 45 (900:20), получим:
Вычитая из второго уравнения первое, узнаем:1000b=400. Отсюда Следовательно, уравнение связи, описывающее зависимость урожайности от качества земель, имеет следующее выражение: Параметр «a» - это постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр «b» показывает среднее изменение результативного признака с изменением величины факторного признака на единицу его измерения. Уравнение регрессии дает возможность определить выравненные (теоретические) значения результативного признака (yx) для каждой единицы исследуемой совокупности. Это достигается подстановкой в данное уравнение соответствующих значений x. Пример. Чтобы рассчитать урожайность зерновых культур для первого хозяйства при качестве почвы 32 балла, необходимо значение x1 подставить в приведенное уравнение:
Найденная величина показывает, какова была бы урожайность при качестве пашни 32 балла, если бы данное хозяйство использовало свои объективные производственные возможности в такой степени, как в среднем все предприятия района. Аналогичные расчеты произведены для каждого хозяйства исследуемой совокупности. Результаты расчетов приведены в последней графе табл.3 Сопоставление фактически достигнутого уровня урожайности с расчетным (теоретическим) позволит оценить результаты работы отдельных хозяйств. По такому же принципу решается уравнение связи при криволинейной зависимости между изучаемыми явлениями. Если с увеличением одного признака значения другого возрастают до определенного предела, а потом начинают снижаться, например, зависимость выработки рабочего от их возраста, то для записи такой зависимости больше всего подходит парабола второго порядка:
Согласно требованиям наименьших квадратов для нахождения параметров «a», «b», «c» данного уравнения нужно решить следующую систему уравнений:
Значение Решают эту систему методом определителей или методом исключения.
|





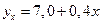 . С увеличением качества почвы на один балл урожайность зерновых культур с 1 га повышается на 0,4ц.
. С увеличением качества почвы на один балл урожайность зерновых культур с 1 га повышается на 0,4ц.
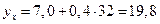


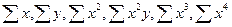 находят на основании исходных данных таким образом, как и в выше приведенном примере.
находят на основании исходных данных таким образом, как и в выше приведенном примере.


