Характеристика одномерных вариационных рядов
В нашем примере самый высокий коэффициент вариации по Используя самый высокий коэффициент вариации, можно определить необходимый объем выборки (
Где
Следовательно, принятый в расчет объем выборки (40 предприятий) является вполне достаточным для проведения корреляционного анализа и для получения объективных результатов. Если связь всех факторов с результативным показателем носит прямолинейный характер, то для описания модели используют линейную функцию:
Если связь носит криволинейный характер, то может быть использована степенная функция: логарифмическая функция:
Приведенные модели удобны тем, что их параметры В линейной модели коэффициенты Коэффициенты Кроме данных моделей могут быть использованы кинетическая, параболическая и другие типы в зависимости от формы связи. Если трудно обосновать форму зависимости, то решение можно произвести по различным функциям и сопоставить полученные результаты. Адекватность различных моделей фактически сложившимся зависимостям проверяется по критерию Фишера, по показателю средней ошибки аппроксимации, и по величине множественного коэффициента детерминации. Чем выше величина критерия Фишера и коэффициента множественной детерминации и чем ниже средняя ошибка аппроксимации, тем точнее данная функция описывает изучаемую зависимость. Исследование взаимосвязей между отобранными факторами и уровнем рентабельности показало, что все зависимости имеют прямолинейный характер. Поэтому для описания данной корреляционной модели может быть использована линейная функция. Примерные модели многофакторного корреляционного анализа основных показателей хозяйственной деятельности сельскохозяйственных предприятий
|

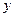
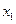


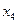
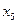
 =22,98) но он не превышает 33%. Следовательно, исходная совокупность данных является однородной и ее можно использовать для дальнейших расчетов.
=22,98) но он не превышает 33%. Следовательно, исходная совокупность данных является однородной и ее можно использовать для дальнейших расчетов. ) по следующей формуле
) по следующей формуле

 - показатель достоверности связи, который при уровне вероятности
- показатель достоверности связи, который при уровне вероятности 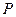 =0,05 равен 1,96;
=0,05 равен 1,96;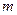 - показатель точности (для экономических расчетов следует принимать 5-8%)
- показатель точности (для экономических расчетов следует принимать 5-8%)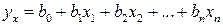


 поддаются экономической интерпретации.
поддаются экономической интерпретации.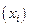 отражают уровень регрессии. Они показывают, на сколько единиц изменяется функция (в абсолютном выражении) с изменением определенного фактора на одну единицу его измерения при неизменном значении остальных аргументов.
отражают уровень регрессии. Они показывают, на сколько единиц изменяется функция (в абсолютном выражении) с изменением определенного фактора на одну единицу его измерения при неизменном значении остальных аргументов.


