Параметры этого уравнения экономического смысла не имеют.
Подставив в это уравнение соответствующее значение На основании этих данных видим, что выработка рабочих повышается до 40-летнего возраста, после чего начинает снижаться. Следовательно, те предприятия, которые имеют больше рабочих 30-40-летнего возраста, будут иметь более высокие показатели производительности труда при прочих равных условиях. Этот фактор необходимо учитывать при планировании уровня производительности труда и при подсчете резервов его роста. При более сложном характере зависимости между изучаемыми признаками для их описания применяются более сложные параболы (третьего, четвертого порядка и т.д.), а также степенная функция, показательная и др. Кроме параболы для записи криволинейных зависимостей в корреляционном анализе применяется гипербола следующего вида:
Для нахождения ее параметров необходимо решить в данном случае следующую систему уравнений:
Гипербола описывает такую зависимость между двумя признаками, когда с увеличением одной переменной значение второй увеличиваются до определенной точки, а потом увеличение происходит более замедленными темпами или вообще не происходит, например, зависимость урожайности от количества вносимых удобрений; от количества осадков; зависимость продуктивности скота от уровня кормления и др. Таким образом, используя тот или иной тип математического уравнения, можно описать степень зависимости между изучаемыми явлениями. Следует отметить, что регрессионный анализ является основной частью корреляционного. Он позволяет только решить первую задачу корреляционного анализа – узнать, на сколько единиц изменяется в среднем признак с изменением другого на одну единицу в абсолютном выражении, но он не отвечает на вопрос, тесная эта связь или нет, решающий фактор это по отношению к результативному показателю или второстепенный. Вторая задача – измерение тесноты связи между факторами и результативными явлениями – решается путем исчисления относительного показателя - коэффициента корреляции, который позволяет судить о силе этой зависимости. Расчет коэффициента корреляции в случае прямолинейной зависимости между изучаемыми признаками производится по следующей формуле:
Коэффициент корреляции по абсолютной величине может принимать значения в пределах от нуля до единицы. Чем ближе его величина к единице, тем теснее связь между изучаемыми явлениями, и наоборот. Пример. Подставив значения
В данном случае величина коэффициента корреляции является существенной Что касается измерения тесноты связи при криволинейной форме зависимости, то здесь используется не линейный коэффициент корреляции, а корреляционное отношение, формула которого имеет следующий вид:
Этот показатель является универсальным. Его можно использовать при любой форме зависимости. Однако, для его нахождения требуется предварительное решение уравнения регрессии и расчет теоретических (выравненных значений) результативного признака Пример. Используя данные этой таблицы, определим корреляционное отношение для нашего примера с помощью следующего расчета: Таблица 5
Подставив полученные значения в формулу, получим:
Если же предположить, что связь между выработкой и возрастом рабочих прямолинейная и определить ее степень с помощью линейного коэффициента корреляции, то, как показывают приведенные ниже расчеты, она совсем незначительная:
В данномслучае форма кривой линии регрессии была выбрана правильно. Правильность этого выбора подтверждает и высокий показатель связи, полученный в результате вычисления корреляционного отношения. Этот показатель оказался значительно большим, чем коэффициент корреляции, вычисленный при предположении линейной формы связи. Расхождение вызвано тем, что кривая линия регрессии значительно точнее описывает зависимость между выработкой рабочих и их возрастом, чем уравнение прямой линии. Таким образом, от правильного выбора уравнения регрессии зависит точность расчетов и обоснованность выводов по результатам анализа. В заключение следует отметить, что мы рассмотрели использование парной корреляции только на двух примерах. Изложенная же методика может быть использована для исследования взаимосвязей между различными экономическими показателями, что позволяет значительно углубить познания об изучаемых явлениях, определить место и роль каждого фактора в формировании уровня результативного показателя.
3. Методика моделирования множественных корреляционных зависимостей
Многофакторный корреляционный анализ можно свести в основном к следующим этапам: 1. Определение факторов, влияющих на изучаемый показатель, и отбор наиболее существенных из них для корреляционной модели. 2.Сбор и статистическая оценка исходной информации, необходимой для корреляционного анализа. 3. Изучение характера связи между отобранными факторами и результативными признаками и обоснование типа математического уравнения, наиболее правильно выражающего сущность исследуемой зависимости. 4. Расчет показателей связи. 5.Оценка результатов корреляционного анализа и практическое применение их. Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно сделан отбор факторов, зависит правильность выводов и обобщений по результатам анализа. Главная роль при отборе факторов для включения их в корреляционную модель принадлежит теории, а также практическому опыту анализа. При этом следует соблюдать следующие условия: 1) при подборе факторов, в первую очередь, следует учитывать причинно-следственные отношения между явлениями, т.к. только познание причинных связей раскрывает сущность изучаемых явлений. Анализ же таких факторов, которые находятся только в соотношении с результативным показателем, не может дать представления о сущности взаимосвязи, не раскрывает в полной мере их внутренней закономерности и поэтому не имеет практического смысла; 2) при создании многофакторной корреляционной модели следует отбирать самые существенные факторы, которые позволяют воспроизвести основные свойства моделируемого явления, ибо учесть и воспроизвести все условия и обстоятельства практически невозможно. Факторы, имеющие критерий надежности меньше табличного, не рекомендуется включать в расчет; 3) все факторы, включаемые в модель, должны быть количественно измеримыми, т.е. иметь единицу измерения; 4) в корреляционную модель линейного типа не следует включать факторы, связь которых с результативным, показателем, носит ярко выраженный криволинейный характер. 5) не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из факторов следует исключить из расчета, ибо это приведет к искажению результатов анализа. Поэтому при построении многофакторной корреляционной модели следует брать в расчет факторы одного уровня. 6) Нельзя включать в корреляционный расчет факторы, связь которых с результативным- показателем носит функциональный характер, т.е. те факторы, алгебраическая сумма или произведение которых равно единице (или 100%). Большую помощь при подборе факторов для корреляционной модели оказывают аналитические группировки как по факторным; так и по результативным признакам. С их помощью можно обосновать наличие, направление, форму связи между изучаемыми показателями. При небольшом объеме выборки для установления связи между факторами и результативным показателем можно воспользоваться приемом сопоставления параллельных и динамических рядов, ранжируя данные по результативному признаку. Одним из приемов установления наличия и форм связи являются линейные графики, таблицы сопряженности, которые позволяют нагляднее изобразить сложившиеся зависимости между факторными и результативными признаками. Отбор факторов может производиться также в процессе решения задачи корреляционного анализа на основе оценки их значимости по ряду критериев, которые будут рассмотрены ниже. Пример. Исходя из перечисленных выше требований и используя названные приемы отбора факторов, для многофакторной корреляционной модели уровня рентабельности продукции (y) отобраны следующие факторы, которые оказывают наиболее существенное влияние на ее уровень:
Поскольку корреляционная связь с достаточной четкостью и полнотой проявляется лишь в массе случаев, количество наблюдений должно быть достаточно велико, так как только в массе наблюдений сглаживайся влияние побочных факторов. Массовость изучаемых явлений и объектов в корреляционном анализе рассматривается как необходимое условие получения достоверных данных. Чем большая совокупность исследуется, тем точнее результаты анализа. Учитывая это требование, влияние перечисленных выше факторов на уровень рентабельности исследуется на примере 40 организаций (можно по 2-3 организациям за 3-5 лет). Следующим этапом анализа является сбор и статистическая оценка исходной информации, которая будет использована для корреляционного анализа. Собранная исходная информация должна быть проверена на достоверность, на однородность, на соответствие закону нормального распределения. При отборе информации для корреляционной модели прежде всего необходимо убедиться в ее достоверности, т.е. соответствии ее объективной действительности. Использование недостоверной информации приведет к неправильным выводам по результатам анализа. Одним из условий, обеспечения точности расчетов в корреляционном анализе является однородность исследуемой информации относительно распределения ее вокруг среднего уровня. Если в совокупности имеются группы объектов с существенно различной силой влияния каких-либо факторов, то это свидетельствует о неоднородности исходной информации Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному признакам. Среднеквадратическое отклонение показывает абсолютное отклонение значений от средней арифметической. Оно определяется по формуле:
Коэффициент вариации показывает относительную меру колеблемости отдельных значений от средней арифметической. Он рассчитывается по формуле:
Чем больше коэффициент вариации, тем относительно больше пестрота и меньше выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если коэффициент вариации не превышает 10%, средней - если выше 10% и значительной - если коэффициент вариации больше 20%, но не превышает 33%. Если Выявление и устранение количественной неоднородности информации - сложный процесс, который требует глубокого профессионально-теоретического анализа исследуемых объектов и моделируемых связей. Следующим требованием, предъявляемым к исходной информации, является ее подчинение закону нормального распределения. Согласно закону нормального распределения основная масса исследуемых данных (вариант) по каждому признаку должна быть сгруппирована вокруг среднего значения ее. График плотности нормального распределения показывают нормальной кривой, которая представляет собой колоколообразную фигуру, симметричную относительно прямой
Для количественной оценки степени отклонения информации от нормального распределения служит отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке. Показатель асимметрии вычисляется по формуле:
а ошибка асимметрии равна:
Показатель эксцесса равен,
и его ошибка
В симметричном распределении А=0. Отличие от нуля указывает не асимметрию в расположении вариант вокруг средней арифметической. Отрицательная асимметрия свидетельствует о том, что преобладают варианты с большими значениями, а варианты с малыми значениями встречаются реже. Положительная асимметрия свидетельствует о преобладании вариант с малыми значениями, а варианты с большими значениями встречаются реже. В нормальном распределении показатель эксцесса Е=0. Если Е = 0, то варианты густо сгруппированы вокруг средней, образуя островершинность кривой распределения по сравнению с нормальной кривой. При Е=0 кривая будет плосковершинной. Симметричные кривые распределения, не имеющие ни положительного, ни отрицательного эксцесса, называются кривыми нормального распределения. Кривые этой формы получаются в том случае, когда все причины, вызывающие отклонение данного свойства от некоторой средней в ту или другую сторону, действуют в одинаковой мере. Если отношение В нашем примере (см. табл. 6) во всех случаях отношение После отбора факторов и оценки исходной информации на однородность и на соответствие закону нормального распределения важной задачей в корреляционном анализе является выбор функции, описывающей модель. Для обоснования функции, также как и для обоснования наличия связи между признаками, используются аналитические группировки, графики, таблицы сопряженность и др.
|

 и
и 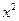 , рассчитываем выравненные значения выработки в зависимости от возраста рабочих
, рассчитываем выравненные значения выработки в зависимости от возраста рабочих  . Результаты расчетов приведены в последней графе таблицы 4.
. Результаты расчетов приведены в последней графе таблицы 4.
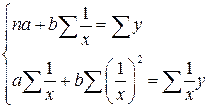

 в формулу из табл.3
в формулу из табл.3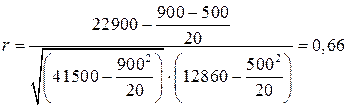
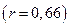 . Это позволяет сделать вывод, что плодородие земель является одним из основных факторов, от которых в данном районе зависит уровень урожайности зерновых культур. Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации
. Это позволяет сделать вывод, что плодородие земель является одним из основных факторов, от которых в данном районе зависит уровень урожайности зерновых культур. Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации  . Он показывает, что урожайность зерновых культур в районе на 43,5% зависит от плодородия земель, а на долю других факторов приходится 56,5% изменения урожайности.
. Он показывает, что урожайность зерновых культур в районе на 43,5% зависит от плодородия земель, а на долю других факторов приходится 56,5% изменения урожайности. , где
, где  ;
; 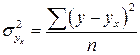 .
.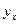 (см. гр.9 в табл. 4).
(см. гр.9 в табл. 4).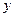



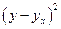
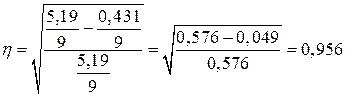
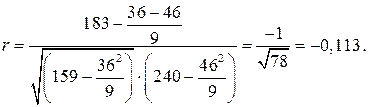
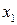 - материалоотдача (производство валовой продукции на 1 руб. материалов), руб.
- материалоотдача (производство валовой продукции на 1 руб. материалов), руб.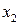 - фондоотдача основных средств, в руб.
- фондоотдача основных средств, в руб. - производительности труда (производство продукции на одного среднегодового работника), млн.руб.
- производительности труда (производство продукции на одного среднегодового работника), млн.руб.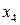 - продолжительность оборота краткосрочных активов, дни
- продолжительность оборота краткосрочных активов, дни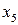 - удельный вес продукции высшей категории качества (засоренность, упитанность, жирность и др.), в %.
- удельный вес продукции высшей категории качества (засоренность, упитанность, жирность и др.), в %.

 выше 33%, то это указывает на неоднородность информации, и ее следует исключить из дальнейшего расчета или отбросить нетипичные в данной выборке наблюдения, которые бывают в первых и последних ранжированных рядах выборки.
выше 33%, то это указывает на неоднородность информации, и ее следует исключить из дальнейшего расчета или отбросить нетипичные в данной выборке наблюдения, которые бывают в первых и последних ранжированных рядах выборки.



 или
или 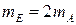
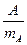 и
и 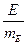 меньше 3, то можно сделать заключение, что асимметрия и эксцесс не имеют существенного значения и что изучаемый признак или фактор подчиняется закону нормального распределения.
меньше 3, то можно сделать заключение, что асимметрия и эксцесс не имеют существенного значения и что изучаемый признак или фактор подчиняется закону нормального распределения.


