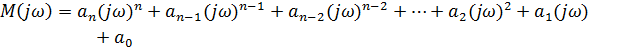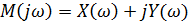Определение устойчивости систем автоматического регулирования по критерию Михайлова.
Критерий позволяет судить об устойчивости САР по очертаниям так называемой кривой Михайлова, представляющей собой годограф вектора M(jw). Для этого необходимо определить характеристическое уравнение замкнутой системы и произвести замену s на jw.В результате замены получаем выражение:
Выделим вещественную и мнимую части вектора Михайлова в выражении:
где
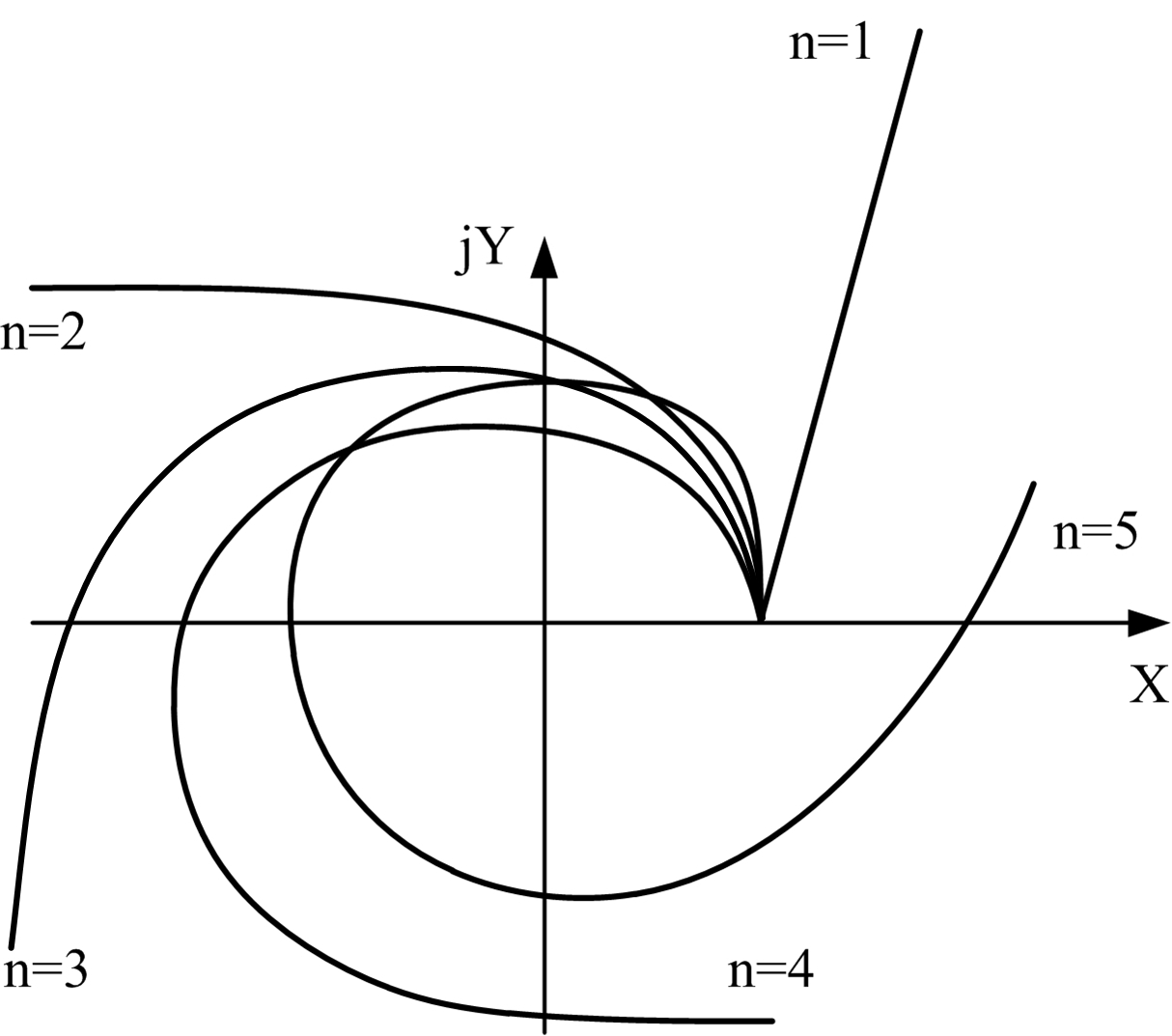
Изменяем частоту w от нуля до бесконечности и строим годограф на комплексной плоскости. Кривая Михайлова строится в плоскости (X, jY) по точкам в соответствии с выражением. Каждой точке кривой соответствует свое значение w. Направление возрастания w обычно указывается стрелкой на кривой. Для устойчивости линейной САР необходимо и достаточно, чтобы вектор M(jw) при изменении w от нуля до бесконечности начинаясь на положительном направлении вещественной оси X повернулся на угол j=pn/2 против часовой стрелки, где n-степень характеристического уравнения замкнутой системы. Таким образом, для практического применения критерия необходимо найти характеристический полином замкнутой системы M(s), построить по точкам кривую Михайлова M(jw) и подсчитать угол j на который поворачивается этот вектор. Если кривая Михайлова имеет плавные спиралеобразные очертания и проходит последовательно n - квадрантов, где n - порядок дифференциального уравнения САР, то такая система будет устойчивой.
|