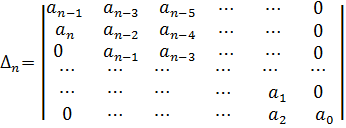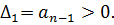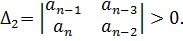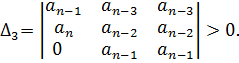Определение устойчивости систем автоматического регулирования по критерию Гурвица.
Формулируется он следующим образом: Пусть характеристическое уравнение замкнутой системы имеет вид:
Тогда для, устойчивости линейной САР необходимо и достаточно, чтобы были положительны n определителей Гурвица ∆1, ∆2,.. ∆n, т.е. чтобы выполнялась система неравенств ∆к > 0, к=1,2,.. n. Определители, о которых идет речь в приведенной формуле, представляют собой диагональные определители (миноры) квадратной матрицы n-ого порядка:
Главный определитель Гурвица составляется по характеристическому уравнению САР по следующему правилу: - по главной диагонали определителя выписываются все коэффициенты характеристического уравнения САР, начиная с an-1; - колонки определителя, начиная от главной диагонали, заполняются коэффициентами с последовательно возрастающими индексами; - все коэффициенты с индексами меньше нуля и с индексами больше степени уравнения заменяются нулями. В соответствии с формулировкой критерия Гурвица диагональные миноры этого определителя должны быть положительными, т.е.:
|