Контрольная работа. «Основы теории эксперимента»
по дисциплине «Основы теории эксперимента»
Работу выполнила студентка: Андреева А.Ф., гр. 9541 Проверил: Кричевский С.В.
Заочное отделение
Самара 2014 1. Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны P1 = 0,1, P2 = 0,15, P3 = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли данная цепь надежной. Так как элементы включены последовательно, то тока в цепи не будет (событие A), если откажет хотя бы один из элементов. Пусть Ai — событие, заключающееся в том, что i-й элемент работает (i = 1, 2, 3). Тогда P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Очевидно, что A1A2A3 — событие, заключающееся в том, что одновременно работают все три элемента, и P(A1A2A3) = P(A1)•P(A2)•P(A3) = 0,612. Тогда P(A) + P(A1A2A3) = 1, поэтому P(A) = 0,388 < 0,4. Следовательно, цепь является надежной.
2. yэ(3) = – 42°, yэ(4) = 0°, yэ(5) = 28°, yэ(6) = 69°. Требуется найти приближенную зависимость между температурой кипения и числом n для этих соединений. Предположим, что эта зависимость имеет вид y» a n + b, где a, b — константы, подлежащие определению. Для нахождения a и b подставим в эту формулу последовательно n = 3, 4, 5, 6 и соответствующие значения температур кипения. Имеем: – 42» 3 a + b, 0» 4 a + b, 28» 5 a + b, 69» 6 a + b. Для определения наилучших a и b существует много разных методов. Воспользуемся наиболее простым из них. Выразим b через a из этих уравнений: b» – 42 – 3 a, b» – 4 a, b» 28 – 5 a, b» 69 – 6 a. Возьмем в качестве искомого b среднее арифметическое этих значений, то есть положим b» 16 – 4,5 a. Подставим в исходную систему уравнений это значение b и, вычисляя a, получим для a следующие значения: a»37, a»28, a»28, a»36. Возьмем в качестве искомого a среднее значение этих чисел, то есть положим a»34. Итак, искомое уравнение имеет вид y» 34n – 139. Проверим точность модели на исходных четырех соединениях, для чего вычислим температуры кипения по полученной формуле: yр(3) = – 37°, yр(4) = – 3°, yр(5) = 31°, yр(6) = 65°. Таким образом, ошибка расчетов данного свойства для этих соединений не превышает 5°. Используем полученное уравнение для расчета температуры кипения соединения с n = 7, не входящего в исходное множество, для чего подставим в это уравнение n = 7: yр(7) = 99°. Результат получился довольно точный: известно, что экспериментальное значение температуры кипения yэ(7) = 98°.
3. Коммивояжеру, живущему в городе A1, надо посетить города A2, A3 и A4, причем каждый город точно один раз, и затем вернуться обратно в A1. Известно, что все города попарно соединены между собой дорогами, причем длины дорог bij между городами Ai и Aj (i, j = 1, 2, 3, 4) таковы: b12 = 30, b14 = 20, b23 = 50, b24 = 40, b13 = 70, b34 = 60.
Изобразим каждый город точкой на плоскости и пометим ее соответствующей меткой Ai (i = 1, 2, 3, 4). Соединим эти точки отрезками прямых: они будут изображать дороги между городами. Для каждой «дороги» укажем ее протяженность в километрах (рис. 2). Получился граф — математический объект, состоящий из некоторого множества точек на плоскости (называемых вершинами) и некоторого множества линий, соединяющих эти точки (называемых ребрами). Более того, этот граф меченый, так как его вершинам и ребрам приписаны некоторые метки — числа (ребрам) или символы (вершинам). Циклом на графе называется последовательность вершин V1, V2,..., Vk, V1 такая, что вершины V1,..., Vk — различны, а любая пара вершин Vi, Vi+1 (i = 1,..., k – 1) и пара V1, Vk соединены ребром. Таким образом, рассматриваемая задача заключается в отыскании такого цикла на графе, проходящего через все четыре вершины, для которого сумма всех весов ребер минимальна. Найдем перебором все различные циклы, проходящие через четыре вершины и начинающиеся в A1: 1) A1, A4, A3, A2, A1; Найдем теперь длины этих циклов (в км): L1 = 160, L2 = 180, L3 = 200. Итак, маршрут наименьшей длины — это первый. Заметим, что если в графе n вершин и все вершины попарно соединены между собой ребрами (такой граф называется полным), то число циклов, проходящих через все вершины, равно
4. В двух группах учащихся — экспериментальной и контрольной — получены следующие результаты по учебному предмету (тестовые баллы; см. табл. 1).[1] Таблица 1. Результаты эксперимента
Общее количество членов выборки: n1=11, n2=9. Расчет средних арифметических: Хср=13,636; Yср=9,444 Стандартное отклонение: sx=2,460; sy=2,186 По формуле (2) рассчитываем стандартную ошибку разности арифметических средних:
Считаем статистику критерия:
Сравниваем полученное в эксперименте значение t с табличным значением с учетом степеней свободы, равных по формуле (4) числу испытуемых минус два (18). Табличное значение tкрит равняется 2,1 при допущении возможности риска сделать ошибочное суждение в пяти случаях из ста (уровень значимости=5 % или 0,05). Если полученное в эксперименте эмпирическое значение t превышает табличное, то есть основания принять альтернативную гипотезу (H1) о том, что учащиеся экспериментальной группы показывают в среднем более высокий уровень знаний. В эксперименте t=3,981, табличное t=2,10, 3,981>2,10, откуда следует вывод о преимуществе экспериментального обучения.
5. Сформулируем нуль-гипотезу Н 0: Мx=Мэ, т.е. математическое ожидание по выборке Мx равно математическому ожиданию эталона Мэ. Решение осуществляется с помощью t-критерия Стьюдента. Для этого рассчитывается экспериментальное (эмпирическое) значение этого критерия по выражению
В дальнейшем определяется теоретическое значение этого критерия при заданном уровне значимости a и числе степеней свободы m=n-1. Для этого опять же можно воспользоваться таблицами из статистических справочников или пакетами прикладных программ для ЭВМ. Характеристики отдельных таких программ, их возможности мы будем изучать в дальнейшем (см. главу 7), а навыки их использования осваивать на практических занятиях. Если tэксп³ta,m, то нуль гипотеза отвергается. Физически это означает, что Таким образом, алгоритм решения задачи следующий: 1. По выборочным данным объема выборки 2. Рассчитывается эмпирическое значение критерия Стьюдента tэксп по выражению (3.26). 3. При a=0,05 и m=n-1 определяется теоретическое значение критерия ta,m. 4. Если ½tэксп½³ta,m, то гипотеза не принимается. 6. При проверке Рh-метра с помощью эталонного раствора, имеющего Рh=9,0, получили следующие результаты: 8,7; 9,2; 9,1; 9,0; 9,4; 9,6; 9,7; 8,9; 8,8; 8,7; 9,8; 9,3; 9,8; 8,8, т.е. n=14. Обладает ли Рh-метр систематической погрешностью? Решение задачи. Предварительно рассчитаем среднеарифметическое
В дальнейшем рассчитывается эмпирическое значение критерия
и определяется табличное значение критерия t0,05;13=2,16. Так как tэксп<ta,m, то с вероятностью 95% можно считать, что имеющееся различие между показаниями Рh-метра и эталонным значением вызвана случайными причинами и в частности ограниченностью числа измерений.
7. В процессе проведения исследований из партии бетона, замешанной в понедельник, взято восемь проб (n1=8) и они подвергнуты испытаниям на сжатие. Получены следующие данные прочности на сжатие, xi(1), кг/см2: 305,6; 270,8; 298,0; 218,6; 273,3; 270,8; 219,4; 265,8. Из партии бетона, замешанной в среду, имелась возможность взять 17 проб (n2=17) и после испытаний получены следующие результаты, xi(2), кг/см2: 298,0; 263,4; 288,2; 300,7; 327,9; 303,1; 278,2; 296,0;316,3; 290,7; 318,0; 270,0; 305,6; 320,5; 293,2; 285,5; 316,3. Утверждается, что состав бетона и методика испытаний не изменялись. Выборки 1 и 2 независимы и не взаимосвязаны. 1. Определяются среднеарифметические значения параметра и оценки их дисперсий по каждой из выборок:
2. Определяется средневзвешенная дисперсия (суммарная, выборочная дисперсия)
3. Проверяется нуль-гипотеза "Математические ожидания первой и второй выборок одинаковы". Н0: Mx(1)= Mx(2). 4. Рассчитывается эмпирическое значение критерия Стьюдента
4.Число степеней свободы определятся по выражению mS = n1 + n2 - 2 = 23 (3.30) и определяется теоретическое значений критерия Стьюдента t0,05;23=2,07 (по статистической справочной таблице или с помощью функции СТЬЮДРАСПОБР из электронных таблиц Microsoft Excel). 5. Так как tэксп>ta,m, то с вероятность 95% гипотеза не принимается. Таким образом, справедливость гипотезы, согласно которой обе партии бетона и методика исследования одинаковы по их средним значениям на сжатие, весьма сомнительна (с вероятностью 95%).
8. В серии из десяти измерений (n=10) было получено При Р=0,9, m=n-1=9, поэтому на основе (3.24) и (3.25) имеем
Значения c12 с надежностью a1=(1-Р)/2=0,05 и c22 с надежностью a2=(1+Р)/2=0,95 табулированы и получены нами с помощью статистической функции ХИ2ОБР из электронных таблиц Microsoft Excel. Следовательно, 0,532×5,4×10-3£s£2,707×5,4×10-3 или 2,87×10-3£s£1,46×10-2. Аналогично для Р=0,95 получаем 2,55×10-3£s£1,80×10-2.
9. При обработке 17 пар данных x и y получены следующие значения n=17; Определение значимости коэффициента rxy.
t0,05;15=1,75. Так как tэксп>ta;n-2, то коэффициент корреляции существенен. Определение доверительного интервала. По формулам (4.22) и (4.23) определим величину Z*
и ее среднеквадратичное отклонение
Зададимся вероятностью того, что истинное значение Z отличается от вычисленного на основании оценки коэффициента корреляции Z* не более, чем на dZ. Учитывая нормальный закон распределения Z, имеем при вероятности 95%: dZ=1,96×SZ=1,96×0,267=0,523; 90%: dZ=1,67×0,267=0,446; 99,7%: dZ=3,00×0,267=0,801. Таким образом, истинное значение Z с вероятностью, например 95%, лежит в пределах Z1£Z£Z2, где Z1=1,738-0,523=1,215 и Z2=1,738+0,523=2,261. Этим двум значениям Z соответствуют коэффициенты корреляции, полученные из формулы (4.22) -0,84£rxy£-0,98. Следовательно, доверительные интервалы подтверждают достаточно сильную причинную связь между анализируемыми параметрами. Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными и оценивает тесноту этой связи 10. Эстонский исследователь Я. Микк [1], изучая трудности понимания текста, установил «формулу читаемости», которая представляет собой множественную линейную регрессию:
где х1 - длина самостоятельных предложений в количестве печатных знаков, х2 - процент различных незнакомых слов, х3 - абстрактность повторяющихся понятий, выраженных существительными. Сравнивая между собой коэффициенты регрессии, выражающие степень влияния факторов, можно видеть, что трудность понимания текста определяется прежде всего его абстрактностью. Вдвое меньше (0,27) трудность понимания текста зависит от числа незнакомых слов и практически она совсем не зависит от длины предложении. 11. Предположим, что математическое ожидание содержания кремния в чугуне равно MSi=0,6%, а среднеквадратичное отклонение sSi=0,15%. В этом случае, мы можем быть уверены в том, что величина измеренного содержания кремния в чугуне будет находиться в интервалах: 0,6 ± 0,68 ´ 0,15 = 0,6±0,10 с вероятностью 68%; 0,6 ± 1,64 ´ 0,15 = 0,6±0,29 с вероятностью 90%; 0,6 ± 1,96 ´ 0,15 = 0,6±0,29 с вероятностью 95%; 0,6 ± 3,00 ´ 0,15 = 0,6±0,45 с вероятностью 99,7%, т.е. из 1000 проб только 3 пробы по содержанию кремния в чугуне будут выходить из диапазона от 0,15 до 1,05%. 12. Пирометром измеряется температура поверхности нагретого тела. Будем предполагать, что температура видимой поверхности нагретого тела во всех точках одинакова. Различными исследователями было проведено шесть измерений температуры и получены следующие их значения: Температура, 0С: 925, 950, 975, 1000, 1025, 1050 (n=6). Имеются ли среди этих измерений грубые погрешности? Предварительно вычислим оценки
Для определения Sx использовали (n-1), т.к. истинное значение измеряемой температуры нам не известно. Заметим, что здесь это важно, т.к. сделано мало измерений (всего n=6). Выберем измерения, имеющие наибольшее отклонение от среднеарифметического значения. Таких значений оказалось два: 925 0C и 1050 0C. Предварительно вычислим
При a=0,05 и m=n-1=5 определяем t0,05;5=2,57 (например, с помощью функции СТЬЮДРАСПОБР(0,05;5)=2,57 из электронных таблиц Excel). Так как tэксп<ta,m, то от отсева выделяющихся наблюдений лучше воздержаться. Попытайтесь самостоятельно оценить, каким должно быть значение измеряемого параметра, чтобы его можно отнести к грубой погрешности при доверительной вероятности 0,997. Заметим дополнительно, что если бы число наблюдений было достаточно большим и было бы известно действительное значение измеряемой температуры, при условии нормального закона распределения t*0,05=1,96, что соответствует теоретическому значению при доверительной вероятности равной 0,95. В нашем случае табличное значение tэксп=2,57 было существенно выше 1,96, т.к. оно учитывало ограниченность экспериментальных данных. 13. Было отобрано 16 проб одного и того же чугуна, в которых определено содержание кремния. В дальнейшем рассчитали
Таким образом, с вероятностью 95% можно утверждать, что математическое ожидание (среднее значение) содержания кремния в чугуне лежит в диапазоне 0,59%£MSi£0,71%.
14. В серии из десяти измерений (n=10) было получено При Р=0,9, m=n-1=9, поэтому имеем
Значения c12 с надежностью a1=(1-Р)/2=0,05 и c22 с надежностью a2=(1+Р)/2=0,95 табулированы и получены нами с помощью статистической функции ХИ2ОБР из электронных таблиц Microsoft Excel. Следовательно, 0,532×5,4×10-3£s£2,707×5,4×10-3 или 2,87×10-3£s£1,46×10-2. Аналогично для Р=0,95 получаем 2,55×10-3£s£1,80×10-2. 15. При проверке Рh-метра с помощью эталонного раствора, имеющего Рh=9,0, получили следующие результаты: 8,7; 9,2; 9,1; 9,0; 9,4; 9,6; 9,7; 8,9; 8,8; 8,7; 9,8; 9,3; 9,8; 8,8, т.е. n=14. Обладает ли Рh-метр систематической погрешностью? Решение задачи. Предварительно рассчитаем среднеарифметическое
В дальнейшем рассчитывается эмпирическое значение критерия
и определяется табличное значение критерия t0,05;13=2,16. Так как tэксп<ta,m, то с вероятностью 95% можно считать, что имеющееся различие между показаниями Рh-метра и эталонным значением вызвана случайными причинами и в частности ограниченностью числа измерений. 16. В процессе проведения исследований из партии бетона, замешанной в понедельник, взято восемь проб (n1=8) и они подвергнуты испытаниям на сжатие. Получены следующие данные прочности на сжатие, xi(1), кг/см2: 305,6; 270,8; 298,0; 218,6; 273,3; 270,8; 219,4; 265,8. Из партии бетона, замешанной в среду, имелась возможность взять 17 проб (n2=17) и после испытаний получены следующие результаты, xi(2), кг/см2: 298,0; 263,4; 288,2; 300,7; 327,9; 303,1; 278,2; 296,0;316,3; 290,7; 318,0; 270,0; 305,6; 320,5; 293,2; 285,5; 316,3. Утверждается, что состав бетона и методика испытаний не изменялись. Выборки 1 и 2 независимы и не взаимосвязаны. 1. Определяются среднеарифметические значения параметра и оценки их дисперсий по каждой из выборок:
2. Определяется средневзвешенная дисперсия (суммарная, выборочная дисперсия)
4. Рассчитывается эмпирическое значение критерия Стьюдента
4.Число степеней свободы определятся по выражению mS = n1 + n2 - 2 = 23 и определяется теоретическое значений критерия Стьюдента t0,05;23=2,07 (по статистической справочной таблице или с помощью функции СТЬЮДРАСПОБР из электронных таблиц Microsoft Excel). 5. Так как tэксп>ta,m, то с вероятность 95% гипотеза не принимается. Таким образом, справедливость гипотезы, согласно которой обе партии бетона и методика исследования одинаковы по их средним значениям на сжатие, весьма сомнительна (с вероятностью 95%). 17. Пусть измеряем одну и ту же величину (температуру, давление, состав газа и т.п.). Старым измерительным прибором проведено 200 измерений, которые дали выборочную дисперсию Sx2(1)=3,82, а вторым (новым) выполнено 15 измерений при выборочной дисперсии Sx2(2)=2,00. Можно ли считать, что новый прибор по разбросу показаний дает существенно лучшую точность, чем старый? Выдвигается гипотеза о равенстве дисперсий. Н0: s x2(1)=s x2(2). Альтернативная ей гипотеза Н1: sx2(1)>s x2(2). Далее определяем: Fэксп=3,82/2,00=1,91; m1=199; m2=14; F0,05;199;14=2,16; Fэксп<Fтеор. Таким образом, с вероятностью 95% нет оснований считать, что результаты измерений нового прибора лучше старого. 18. При обработке 17 пар данных x и y получены следующие значения n=17; Определение значимости коэффициента rxy.
t0,05;15=1,75. Так как tэксп>ta;n-2, то коэффициент корреляции существенен. Определение доверительного интервала. По формулам (4.22) и (4.23) определим величину Z*
и ее среднеквадратичное отклонение
Зададимся вероятностью того, что истинное значение Z отличается от вычисленного на основании оценки коэффициента корреляции Z* не более, чем на dZ. Учитывая нормальный закон распределения Z, имеем при вероятности 95%: dZ=1,96×SZ=1,96×0,267=0,523; 90%: dZ=1,67×0,267=0,446; 99,7%: dZ=3,00×0,267=0,801. Таким образом, истинное значение Z с вероятностью, например 95%, лежит в пределах Z1£Z£Z2, где Z1=1,738-0,523=1,215 и Z2=1,738+0,523=2,261. Этим двум значениям Z соответствуют коэффициенты корреляции, полученные из формулы (4.22) -0,84£rxy£-0,98. Следовательно, доверительные интервалы подтверждают достаточно сильную причинную связь между анализируемыми параметрами. 19. Пусть требуется определить объем цилиндра диаметром d=20 мм и высотой h=50 мм с относительной погрешностью DV*=0,01, соответствующей доверительной вероятностью P=0,95. Найдем погрешности измерения величины d и h, соответствующие этому же значению доверительной вероятности, при которых исходная задача будет разрешена. Учитывая, что объем цилиндра равен
|

 Рассмотрим несколько химических соединений, называемых нормальными алканами. Они состоят из n атомов углерода и n + 2 атомов водорода (n = 1, 2...), связанных между собой так, как показано на рисунке 3 для n = 3. Пусть известны экспериментальные значения температур кипения этих соединений:
Рассмотрим несколько химических соединений, называемых нормальными алканами. Они состоят из n атомов углерода и n + 2 атомов водорода (n = 1, 2...), связанных между собой так, как показано на рисунке 3 для n = 3. Пусть известны экспериментальные значения температур кипения этих соединений: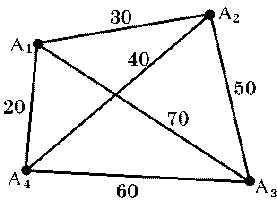 Надо определить порядок посещения городов, при котором длина соответствующего пути минимальна.
Надо определить порядок посещения городов, при котором длина соответствующего пути минимальна.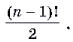 Следовательно, в нашем случае имеется ровно три цикла.
Следовательно, в нашем случае имеется ровно три цикла.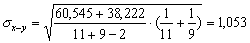

 (3.26)
(3.26)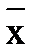 не покрывается доверительным интервалом Mx с вероятностью Р=1-a.
не покрывается доверительным интервалом Mx с вероятностью Р=1-a. находятся Sx2.
находятся Sx2.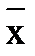 и выборочное среднеарифметическое отклонение Sx
и выборочное среднеарифметическое отклонение Sx
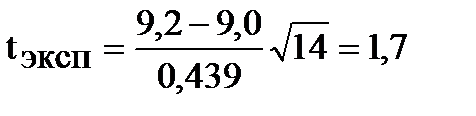
 =265,3;
=265,3;  =298,3;
=298,3;  =1015,1;
=1015,1;  =329,1.
=329,1.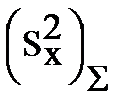 :
: (3.28)
(3.28)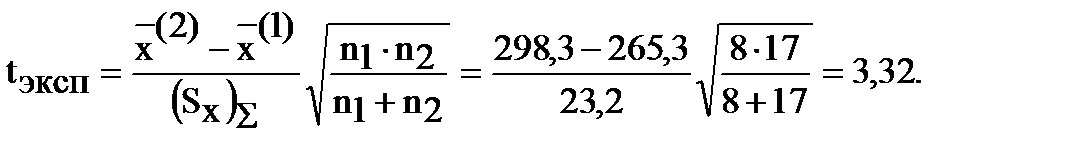 (3.29)
(3.29) =5,4×10-3 мм2. Требуется определить, в каком интервале находится фактическое значение дисперсии s.
=5,4×10-3 мм2. Требуется определить, в каком интервале находится фактическое значение дисперсии s.
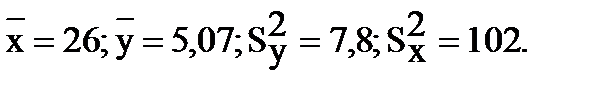 Выборочный коэффициент корреляции rxy=-0,94, т.е. величина y связана с x достаточно сильной причинной связью, близкой к функциональной зависимости.
Выборочный коэффициент корреляции rxy=-0,94, т.е. величина y связана с x достаточно сильной причинной связью, близкой к функциональной зависимости. ;
;

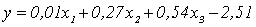 — оценка трудности понимания текста,
— оценка трудности понимания текста, и S:
и S:

 =0,65% и Sx=0,11%. Теоретическое значение критерия Стьюдента составило t0,05;15=2,13. Тогда
=0,65% и Sx=0,11%. Теоретическое значение критерия Стьюдента составило t0,05;15=2,13. Тогда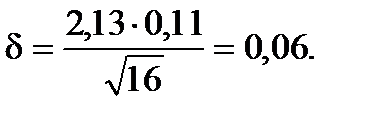
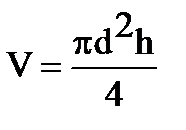 и приняв закон распределения нормальным, с помощью соотношения (5.16) найдем
и приняв закон распределения нормальным, с помощью соотношения (5.16) найдем



