Температура и её физический смысл

Уравнение состояния идеального газа

Основным уравнением, описывающим поведение идеального газа, является уравнение Менделеева-Клапейрона (уравнение состояния идеального газа):

p ⋅ V = ν;⋅ R ⋅ T,

где p — давление газа, V — объем, занимаемый газом, ν; — количество моль газа, ν; — абсолютная температура газа (размерность — K), R =8,31 Джмоль⋅К — универсальная газовая постоянная.

Это уравнение можно написать в различных формах. В форме Менделеева-Клапейрона написано выше. Например, в форме Больцмана p = n ⋅ k ⋅ T, где n = NV — концентрация газа, k =1,38⋅10−23 ДжК — постоянная Больцмана. Важно знать, что R = k ⋅ Na!

Напоминаем, что все приведенные уравнения справедливы только для идеального газа (для реальных газов, близких к идеальным). В остальных случаях наблюдаются отклонения от газовых законов, вызванные взаимодействием молекул и конечностью их суммарного объема.

Кроме того, будьте внимательны в случаях, когда с газами происходят химические реакции, диссоциация или из-за утечек или конденсации не сохраняется количество газа. В формулах ν; — количество именно газа, а не содержимого сосуда!

 

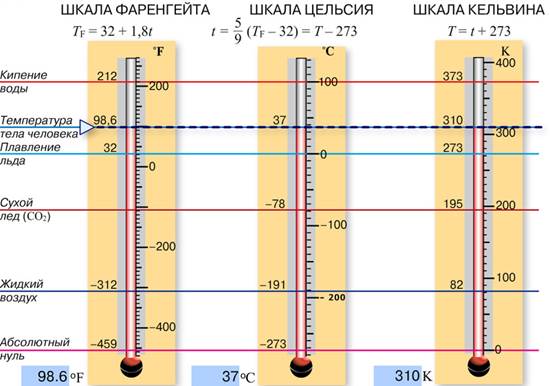
Температура и её физический смысл

Особенно упрощаются газовые законы, если использовать абсолютную температуру (по шкале Кельвина).

Абсолютная температура, или температура по шкале Кельвина T является количественной мерой средней кинетической энергии хаотического поступательного движения молекул и определяется по формуле:

E ¯¯=32 k ⋅ T,

где k =1,38⋅10−23 ДжК − постоянная Больцмана, которая является переводным коэффициентом между единицами абсолютной температуры и единицами кинетической энергии.

Между шкалами Кельвина T и Цельсия t существует простая связь:

T = t +273.

Температура по шкале Кельвина может быть только положительной, так как она пропорциональна кинетической энергии молекул. Абсолютный нуль соответствует по шкале Цельсия температуре t =–2730C.