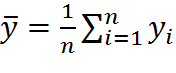ОЦЕНКА ТЕСНОТЫ ЛИНЕЙНОЙ СВЯЗИ
КОРРЕЛЯЦИЯ, ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КОРРЕЛЯЦИИ ОЦЕНКА ТЕСНОТЫ ЛИНЕЙНОЙ СВЯЗИ Экономические данные представляют собой количественные характеристики каких-либо экономических объектов или процессов. Они формируются под действием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обусловливать случайность данных, которые они определяют. Одной из основных задач в экономических исследованиях является анализ зависимостей между переменными. Выделим два типа связей: Функциональные – характеризуются полным соответствием между изменением факторного признака и изменением результативной величины: каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Этот тип связи выражается в виде формульной зависимости. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками.
Корреляционные – между изменением двух признаков нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем, при массовом наблюдении фактических данных.
Одновременное воздействие на изучаемый признак большого количества разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значении результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия. Следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. Изучая взаимосвязи между признаками, их классифицируют по направлению, форме, числу факторов: По направлению связи делятся на прямые и обратные. При прямой связи направление изменения результативною признака совпадает с направлением изменения признака-фактора. При обратной связи направление изменения результативного признака противоположно направлению изменения признака-фактора.
По форме (виду функции) связи делят на линейные (прямолинейные) и нелинейные (криволинейные). Линейная связь отображается прямой линией, нелинейная – кривой (параболой, гиперболой и т.п.). При линейной связи с возрастанием значения факторного признака происходит равномерное возрастание (убывание) значения результативного признака. По количеству факторов, действующих на результативный признак, связи подразделяют на однофакторные (парные) и многофакторные. Изучение зависимости вариации признака от окружающих условий и составляет содержание теории корреляции. При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит При изучении взаимосвязи между двумя факторами их, как правило, обозначают Ковариация – это статистическая мера взаимодействия двух переменных.
Ковариация между двумя переменными
 , ,
где
Если случайные величины Х и Y независимы, теоретическая ковариация равна нулю. Ковариация зависит от единиц, в которых измеряются переменные Х и Y она является ненормированной величиной. Поэтому для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции.
|

 наблюдений.
наблюдений. и
и 
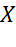 и
и 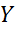 рассчитываетсяследующим образом:
рассчитываетсяследующим образом: – фактические значения переменных
– фактические значения переменных  ,
,