Корреляция
Различные явления, происходящие в процессе сельскохозяйственного производства, находятся в причинно-следственной однофакторной связи, которая может быть функциональной или корреляционной. При функциональной связи каждому значению факторного признака соответствует строго определенное значение результата. Например, связь средней площади питания сельскохозяйственных растений с плотностью их посадки, выручки с количеством проданной продукции при данных ценах и т.п. В отличие от этого при корреляционной связи одному и тому же значению факторного признака могут соответствовать множество различных результатов. Например, связь между уровнем внесения удобрений и урожайностью сельскохозяйственных культур; уровнем кормления, качеством кормов, породностью коров и их молочной продуктивностью; квалификацией работников, обеспеченностью средствами производства и производительностью труда и т.п. Статистикой выработаны специальные приемы установления и измерения такого вида связей, получившие названия метода корреляционного анализа. Они применимы к измерению связей между двумя признаками- парная корреляция или к измерению связей между тремя и большим числом признаков- множественная корреляция. Методы корреляции позволяют решить следующие основные задачи: 1) определить среднее изменение результативного признака под влиянием одного или комплекса факторов (в абсолютном или относительном измерении); 2) охарактеризовать меру зависимости результативного признака и одного из факторов при среднем значении других; 3) определить тесноту связи результативного признака со всем комплексом включенных в анализ факторов или с отдельным фактором при исключении влияния других; 4) статистически оценить выборочные показатели корреляционной связи. Каждая из этих задач решается путем расчета определенных показателей. Применение метода корреляционного анализа включает ряд этапов: 1.Постановка задачи и установление причин связи. Для этого требуется глубокое понимание сущности изучаемых взаимосвязей, так как сам метод не позволяет установить причины возникновения связей между явлениями, его назначение заключается в их количественном измерении. На данном этапе осуществляется общее ознакомление с изучаемым объектом, уточняются задачи исследования, устанавливается теоретическая возможность причинно-следственной связи. 2. Отграничение объекта исследования и отбора необходимых признаков. При отграничении объекта следует иметь в виду, что корреляционный анализ должен проводится лишь в пределах качественно однократных (в социальном, экономическом или производственно-техническом отношении) достаточно многочисленных совокупностей. Отбираемые для корреляционной модели факторные и результативные признаки должны быть существенными, первые должны оказывать непосредственное влияние на вторые. Нежелательно включение в одну модель частных и общих факторов, а также нескольких факторных признаков, находящихся в тесной связи друг с другом. Серьезную помощь для отбора показателей могут оказать результативные и факторные статистические группировки с соответствующим анализом влияния факторов на результативный признак. 3. Установление формы связи и подбор математического уравнения модели связи. Этот вопрос решается на основании теоретического анализа или предшествующим практическим опытом соответствующих исследований. Если форма связи неизвестна, то проводится группировка статистических данных и изучение изменения средних по группам, сопоставление параллельных рядов, построение графиков и таблиц распределения численностей. Уравнения, выражающие статистическую связь, называются уравнениями регрессии или корреляции. Связь между результативным и факторным признаками может носить линейный или криволинейный (параболический, синусоидальный и т.п.) характер. При линейной парной связи между признаками используется уравнение прямой: В случае линейной взаимосвязи результативного признака с несколькими факторами используется множественное линейное уравнение:
где При нелинейной форме связи подбирается соответствующее уравнение криволинейной зависимости, способное наиболее точно отразить имеющуюся связь. Например, форму связи между возрастом коров и их молочной продуктивностью, характеризующуюся тем, что с изменением возраста вначале продуктивность растет, а затем постепенно снижается, можно отразить уравнение параболы второго порядка 4. Расчет числовых характеристик корреляционной связи. Этот этап заключается в нахождении параметров корреляционного уравнения Для получения системы нормальных уравнений записывается исходное корреляционное уравнение. Например, при парной линейной связи уравнение имеет вид:
Для получения второго уравнения каждый член исходного уравнения перемножается на коэффициент при втором неизвестном (
Руководствуясь этими правилами, можно составить любую необходимую систему уравнений. Величины Теснота связи при наличии различных формах зависимости определяется специальными показателями. При парной линейной зависимости- коэффициентом корреляции (
где
При соотношении дисперсий и одинаковом числе наблюдений формула имеет вид:
На основе формулы Наиболее употребительной при парной линейной зависимости является:
При множественной линейной зависимости, если известны коэффициенты парных связей
Линейный парный коэффициент корреляции меняется в пределах от -1 до +1, а множественный коэффициент и индекс корреляции рассматривается только как положительная величина и изменяется в пределах от 0 до 1. Квадрат коэффициента корреляции и индекса корреляции называется коэффициентом детерминации и показывает, на сколько процентов результативный признак зависит от одного или нескольких факторных признаков, включенных в анализ. При изучении связи по выборочным данным полученные коэффициенты регрессии и корреляции должны быть подвергнуты специальной оценке соответствия их показателям генеральной совокупности, так называемой оценке на достоверность. Задача 1. Определение показателей связи при парной линейной зависимости по не сгруппированным данным. По данным об урожайности зерновых культур и качестве Решение Для определения формы связи между урожайностью зерновых культур и качеством почвы построим график (рис.3). На оси абсцисс нанесем значение независимой переменной (качество почвы), на оси ординат- зависимой (урожайность). Расположение точек на поле графика показывает, что связь между признаками линейная, прямо пропорциональная и может быть выражена уравнением прямой линии
Все наблюдаемые расчеты сделаны в табл. 6.1. Подставив их в уравнения, получим:
Таблица. Данные для управления связи и коэффициента корреляции
10 20 30 40 50 60 70 80 90 100 Рис.3. зависимость урожайности от качества почвы Разделим два уравнения на коэффициенты при
Вычтем из большего уравнения меньшее, в данном случае из второго первое: 0,711=4,87 Определим тесноту связи между изучаемыми признаками, рассчитав коэффициент корреляции по формуле:
Для определения коэффициента корреляции надо определить среднее значение
=
Подставим полученные данные в формулу коэффициента корреляции:
Коэффициент парной линейной корреляции можно рассчитать и по другой форме, если известен коэффициент регрессии:
Рассчитанный коэффициент корреляции показал существенную зависимость урожайности зерновых от качества почв. Коэффициент детерминации (
|

 =
= 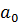 +
+ 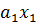 , где
, где 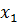 - независимая переменная,
- независимая переменная, 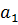 - коэффициент регрессии, показывающий среднее изменение
- коэффициент регрессии, показывающий среднее изменение 
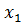 .
.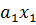 +
+ 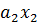 +
+ 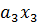 +…+
+…+ 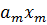 ,
,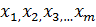 - факторные признаки;
- факторные признаки; 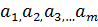 - коэффициенты регрессии, показывающие степень среднего изменения зависимой переменной при изменении факторного признака на единицу при условии, что остальные факторы, включенные в уравнение, остаются неизменными.
- коэффициенты регрессии, показывающие степень среднего изменения зависимой переменной при изменении факторного признака на единицу при условии, что остальные факторы, включенные в уравнение, остаются неизменными. , где коэффициент регрессии
, где коэффициент регрессии 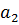 характеризует замедление.
характеризует замедление.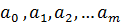 . Для этого составляется система нормальных уравнений, при этом сумма квадратов отклонений фактических данных от исчисленных по уравнению должна быть минимальной, т.е.
. Для этого составляется система нормальных уравнений, при этом сумма квадратов отклонений фактических данных от исчисленных по уравнению должна быть минимальной, т.е. 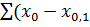 )²= min, где
)²= min, где 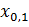 - значение зависимой переменной, исчисленное по сравнению. Этот способ называют методом наименьших квадратов.
- значение зависимой переменной, исчисленное по сравнению. Этот способ называют методом наименьших квадратов.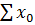 =n
=n 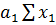 .
.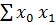 =
= 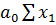 +
+ 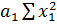 .
.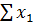 ,
, 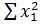 и т.д. рассчитывают по фактическим данным, подставляют их в уравнения и решают систему уравнений, находя неизвестные параметры
и т.д. рассчитывают по фактическим данным, подставляют их в уравнения и решают систему уравнений, находя неизвестные параметры 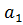 ,
, 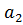 ,…
,… 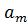 . В настоящее время созданы специальные стандартные программы для решения этих задач на ЭВМ.
. В настоящее время созданы специальные стандартные программы для решения этих задач на ЭВМ.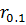 ), при множественной линейной корреляции- коэффициентом множественной корреляции (
), при множественной линейной корреляции- коэффициентом множественной корреляции (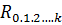 ), при парной криволинейной зависимости- индексом корреляции (i) или корреляционным отношением (ŋ). Во всех случаях показатель тесноты связи определяется отношением:
), при парной криволинейной зависимости- индексом корреляции (i) или корреляционным отношением (ŋ). Во всех случаях показатель тесноты связи определяется отношением: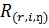 =
= 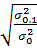 ,
,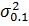 =
= 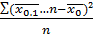 - дисперсия результативного признака под влиянием одного или нескольких факторных;
- дисперсия результативного признака под влиянием одного или нескольких факторных;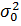 =
= 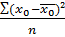 - общая дисперсия результативного признака под влиянием всех факторов(учтенных и неучтенных).
- общая дисперсия результативного признака под влиянием всех факторов(учтенных и неучтенных).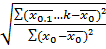 .
.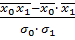 .
.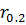 ,
, 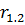 , используют следующую формулу:
, используют следующую формулу: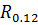 =
= 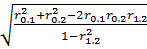 .
. (табл.) необходимо составить и решить корреляционное уравнение, определив параметры уравнения, а также тесноту связи.
(табл.) необходимо составить и решить корреляционное уравнение, определив параметры уравнения, а также тесноту связи.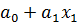 , где
, где 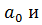
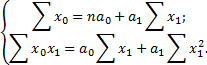
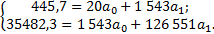
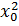
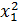
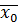
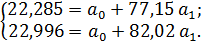
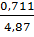 = 0,146. Подставим полученное значение
= 0,146. Подставим полученное значение 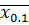 =11,02+0,146
=11,02+0,146 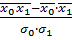 .
.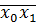 ,
, 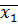 , а также средние квадратические отклонения по результативному и факторному признакам. Все исходные и расчетные данные имеются в табл.
, а также средние квадратические отклонения по результативному и факторному признакам. Все исходные и расчетные данные имеются в табл.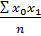 =
= 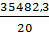 = 1774,11;
= 1774,11;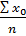 =
= 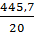 = 22,285;
= 22,285; 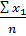 =
= 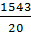 = 77,15;
= 77,15;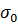 =
= 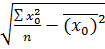 =
= 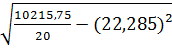 =
= 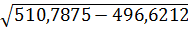 =
= = 3,764;
= 3,764;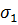 =
= 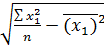 =
= 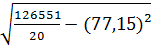 =
=  =
= 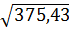 =19,376
=19,376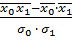 =
= 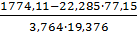 =
= 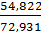 = 0,752.
= 0,752.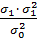 =
=  = 0,752.
= 0,752.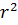 = 0,565) показывает, что на 56,5 % урожайность в данных условиях зависит от качества почвы, а на 44,5 %- от других факторов, которые не были приняты во внимание.
= 0,565) показывает, что на 56,5 % урожайность в данных условиях зависит от качества почвы, а на 44,5 %- от других факторов, которые не были приняты во внимание.


