Несмещенные, эффективные и состоятельные статистические оценки
Тема Статистические оценки параметров распределения Несмещенные, эффективные и состоятельные статистические оценки Одной из центральных задач математической статистики являет задача оценки теоретического распределения случайной величины на основе выборочных данных. При этом предполагается, что закон распределения генеральной совокупности известен, но неизвестны его параметры, такие, например, как математическое ожидание и дисперсия. Требуется найти приближенные значения этих параметров, т. е. получить их статистические оценки. Обозначим через
Это значит, что оценка тоже является случайной величиной. Если для оценки некоторого параметра Несмещенной называется статистическая оценка 0*, математическое ожидание которой равно оцениваемому параметру М ( Смещенной называется оценка Так же как и для любой случайной величины, оценка Эффективно й называется статистическая оценка, которая при одних и тех же объемах выборки имеет наименьшую дисперсию. В некоторых случаях становится интересным поведение оценки при неограниченном увеличении объема выборки. Состоятельной называется статистическая оценка, которая при увеличении объема выборки n стремится по вероятности к оцениваемому параметру, т. е. М (
|

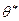 оценку некоторого теоретического параметра
оценку некоторого теоретического параметра 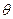 закона распределения случайной величины X. Рассматривая выборочные значения
закона распределения случайной величины X. Рассматривая выборочные значения  как реализации случайных величин
как реализации случайных величин  , получивших конкретные значения в результате опытов, можно представить оценку
, получивших конкретные значения в результате опытов, можно представить оценку  .
.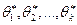 . Математическое ожидание случайной величины
. Математическое ожидание случайной величины 



