Дисперсия числа появлений события в независимых испытаниях
Теорема 9.2 Дисперсия числа появлений события A в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:
Величины
Вычислим дисперсию D ( Величина Найдем математическое ожидание величины Подставляя найденные результаты в соотношение (**), имеем D ( Очевидно, дисперсия каждой из остальных случайных величин также равна pq. Заменив каждое слагаемое правой части (*) через pq, окончательно получим D(X) = npq.
|
.
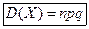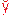Рассмотрим случайную величину X — число появлений события A в n независимых испытаниях. Очевидно, общее число появлений события в этих испытаниях равно сумме появлений события в отдельных испытаниях: 
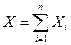, где 
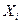- число наступлений события в i -ом испытании.
(*)
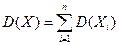по формуле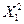
) - (M(
(**)
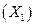= р.
с вероятностью p и 
с вероятностью q: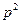
= p(l—p) = pq.
