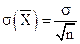Взаимно независимых случайных величин
Пусть известны средние квадратические отклонения нескольких взаимно независимых случайных величин. Как найти среднее квадратическое отклонение суммы этих величин? Ответ на этот вопрос дает следующая теорема. Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:
Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых (следствие 1), поэтому
9.5.Одинаково распределенные взаимно независимые случайные величины Если несколько случайных величин имеют одинаковые распределения, то их числовые характеристики одинаковы. Рассмотрим п взаимно независимых случайных величин Обозначим среднее арифметическое рассматриваемых случайных величин через
Следующие ниже три положения устанавливают связь между числовыми характеристиками среднего арифметического X и соответствующими характеристиками каждой отдельной величины. 1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из
Приняв во внимание, что математическое ожидание каждой из величин по условию равно а, получим
2. Дисперсия среднего арифметического п одинаково распределенных взаимно независимых случайных величий в п раз меньше дисперсии D каждой из величин:
Приняв во внимание, что дисперсия каждой из величин по условию равна D, получим
3. Среднее квадратическое отклонение среднего арифметического п одинаково распределенных взаимно независимых случайных величин в
Вывод:Поскольку дисперсия и среднее квадратическое отклонение служат мерами рассеяния случайной величины, то среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина.
|

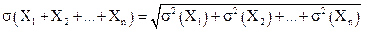
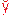 . Обозначим через X сумму рассматриваемых взаимно независимых величин:
. Обозначим через X сумму рассматриваемых взаимно независимых величин: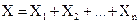
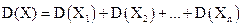
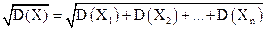

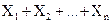 , которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляет изучение числовых характеристик среднего арифметического этих величин.
, которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляет изучение числовых характеристик среднего арифметического этих величин.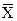 :
: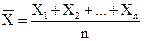
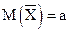
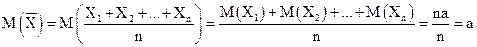
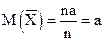
 .
.

 раз меньше среднего квадра-тического отклонения
раз меньше среднего квадра-тического отклонения  каждой из величин:
каждой из величин: