Дисперсия. Свойства дисперсий
Дисперсия вычисляется по формуле
Свойство 1. Дисперсия постоянной величины C равна нулю.
D (С) = 0
Итак, D (С) = 0. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D (СХ) = М {[СХ— М (СХ)]2} = М {С2 [X — М (X)]2} =С2 M{[X — М (X)]2 }= = C2D (X). Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D (X + Y) = М [(X + Y)2] - [М (X + Y)]2= = М (X2) + 2М (X) М(Y) + М (Y2) - М2(X) – 2M(Х)М(Y)- M2(Y) = {М (X2) — [М (X)]2} + {М (Y2) -[M (Y)]2} = D (X) +D (Y). Итак, D (X + Y) = D (X) +D(Y). Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. Например, для трех слагаемых имеем D (X +Y+Z) = D (X) + D(Y) + D(Z). Для произвольного числа слагаемых доказательство проводится методом математической индукции. Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D(X - Y) = D (X) +D(Y).
D(X - Y) = D(X) + D(-Y) = D(X) + (-1
|
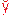D (С) = М (С— М(C) 
= М (С— C 
.
.
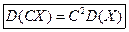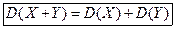