
 существования б) изменение физической величины в одной точке должны вызывать
существования б) изменение физической величины в одной точке должны вызывать
волны:с некоторым запаздыванием изменения этой же величины в
ближайшей окрестности этой точки.
2)  Уравнение волны (простейший случай – волна распространяется вдоль одной прямой 0х)
Уравнение волны (простейший случай – волна распространяется вдоль одной прямой 0х) 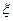
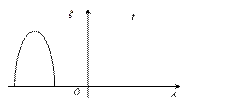
Пусть  - какая либо физическая величина (Е, р,
- какая либо физическая величина (Е, р, 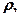 х …),
х …),  - скорость распространения волны.
- скорость распространения волны.
Пусть в точке х=0 физическая величина изменяется по гармоническому закону

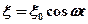 (1),
(1),
где 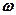 - циклическая частота колебаний источника волны.
- циклическая частота колебаний источника волны.

 В точку с координатой х возмущение придет с запаздыванием на
В точку с координатой х возмущение придет с запаздыванием на  :
:
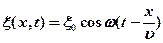 (2) - уравнение гармонической бегущей волны
(2) - уравнение гармонической бегущей волны


 характеристики волны
характеристики волны




амплитуда волны фаза волны период волны ф азовой скоростью 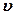
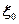

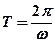 скоростью распространения
скоростью распространения


 определенная фаза колебания
определенная фаза колебания
 длина волны волновое число
длина волны волновое число


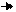
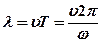
 (3) Фронт волны
(3) Фронт волны
(волновая поверхность)
геомет. место точек, колеб.
в одинаковой фазе
Преобразуем: 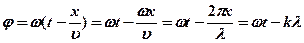

 (2)
(2) 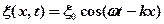 (4)
(4)
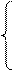
 Словосочетание «колебания частиц совпадают по фазе» используют для тех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции скорости. На самом деле фазы этих частиц отличаются на
Словосочетание «колебания частиц совпадают по фазе» используют для тех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции скорости. На самом деле фазы этих частиц отличаются на 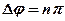 , где n –четное число.
, где n –четное число.
Длиной волны называется расстояние, на которое распространяется волна за период или минимальное расстояние между точками среды, колеблющимися в одинаковой фазе.

Источником волны называется колеблющееся тело, возбуждающее волновое движение.
 В случае волны, распространяющейся вдоль оси 0x для таких точек
В случае волны, распространяющейся вдоль оси 0x для таких точек 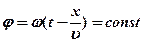 и при
и при 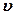 =const,
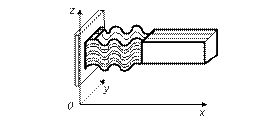
=const, 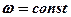 в фиксированный момент времени t x=const, т.е. фронт волны – плоскость, перпендикулярная оси 0x.
в фиксированный момент времени t x=const, т.е. фронт волны – плоскость, перпендикулярная оси 0x.


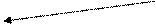 фронт волны
фронт волны


плоский (волна плоская) сферический (волна сферическая)






 существования б) изменение физической величины в одной точке должны вызывать
существования б) изменение физической величины в одной точке должны вызывать Уравнение волны (простейший случай – волна распространяется вдоль одной прямой 0х)
Уравнение волны (простейший случай – волна распространяется вдоль одной прямой 0х) 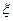

 - какая либо физическая величина (Е, р,
- какая либо физическая величина (Е, р, 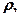 х …),
х …),  - скорость распространения волны.
- скорость распространения волны.
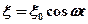 (1),
(1),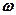 - циклическая частота колебаний источника волны.
- циклическая частота колебаний источника волны.
 В точку с координатой х возмущение придет с запаздыванием на
В точку с координатой х возмущение придет с запаздыванием на  :
: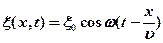 (2) - уравнение гармонической бегущей волны
(2) - уравнение гармонической бегущей волны

 характеристики волны
характеристики волны




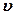
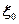

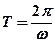 скоростью распространения
скоростью распространения

 определенная фаза колебания
определенная фаза колебания длина волны волновое число
длина волны волновое число

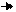
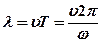
 (3) Фронт волны
(3) Фронт волны
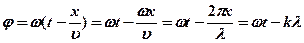

 (2)
(2) 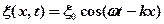 (4)
(4)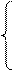
 Словосочетание «колебания частиц совпадают по фазе» используют для тех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции скорости. На самом деле фазы этих частиц отличаются на
Словосочетание «колебания частиц совпадают по фазе» используют для тех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции скорости. На самом деле фазы этих частиц отличаются на 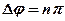 , где n –четное число.
, где n –четное число.
 В случае волны, распространяющейся вдоль оси 0x для таких точек
В случае волны, распространяющейся вдоль оси 0x для таких точек 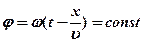 и при
и при 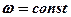 в фиксированный момент времени t x=const, т.е. фронт волны – плоскость, перпендикулярная оси 0x.
в фиксированный момент времени t x=const, т.е. фронт волны – плоскость, перпендикулярная оси 0x.

 фронт волны
фронт волны






