Краткие теоретические сведения. Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и, на первый взгляд, беспорядочно
Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и, на первый взгляд, беспорядочно. Результат каждого отдельного измерения случайной величины практически непредсказуем. Однако совокупности результатов измерений подчиняются статистическим закономерностям, изучение которых служит одной из основ теории и практики физического и инженерного эксперимента. Существует множество законов распределения случайных величин. Одним из наиболее распространенных является нормальный закон распределения, описываемый функцией Гаусса:
Закономерность распределения значений изучаемой случайной величины t становится наглядной, если построить гистограмму - ступенчатую диаграмму, показывающую, как часто при измерениях появляются значения, попадающие в тот или иной из равных интервалов D t, лежащих между наименьшим и наибольшим из наблюдаемых значений величины t. Гистограмму строят в следующих координатах (рис 1): ось абсцисс – измеряемая величина t; ось ординат – Δ N / N Δ t. Здесь N - полное число измерений, Δ N - число результатов, попавших в интервал [ t, t + Δ t ]. Частное Δ N / N - есть доля результатов, попавших в указанный интервал, и характеризует вероятность попадания в него результата отдельного измерения. Отношение этой величины к ширине интервала Δ N / N Δ t называется "плотностью вероятности". При очень большом числе измерений (
Эту функцию называют плотностью вероятности или законом распределения по t. Чтобы сравнить наблюдаемое распределение с нормальным распределением (1), нужно найти по данным измерений параметры <t>; и σ функции Гаусса (приближенно, поскольку число измерений ограничено). Параметр <t>; есть среднее арифметическое случайной величины
Параметр σ является средним квадратичным отклонением наблюдений от среднего <t>;:
Из анализа формулы (1) следует, что плотность нормального распределения имеет максимум
при значении t = <t>; и симметрична относительно < t>;. Нетрудно сравнить “наибольшую высоту гистограммы” и максимальное значение функции Гаусса (5). Для количественной проверки того, насколько хорошо полученные результаты соответствуют нормальному распределению, можно воспользоваться соотношением (6)
в котором вероятность Р 12 попадания результата измерения в интервал (t 1, t 2) c одной стороны может быть вычислена как интеграл функции Гаусса в этих пределах, а с другой стороны - найдена как относительное число наблюдений N 12, результаты которых попали в этот интервал. При сравнении наблюдаемого распределения с нормальным (1) можно воспользоваться известными значениями вероятности распределения случайной величины для наиболее употребительных в технике измерений пределов:
t (<t>; -s; <t>;+s), P s = 0,68;
t (<t>; -2s; <t>;+2s), P 2s = 0,95;
t (<t>; -3s; <t>;+3s), P 3s = 0,997.
|

 , (1)
, (1)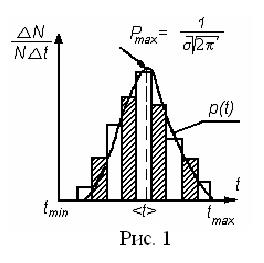 где ρ(t) – плотность нормального распределения случайной величины t, σ – среднеквадратичная ошибка или стандарт.
где ρ(t) – плотность нормального распределения случайной величины t, σ – среднеквадратичная ошибка или стандарт.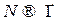 ) вместо ступенчатой гистограммы получается плавная кривая зависимости
) вместо ступенчатой гистограммы получается плавная кривая зависимости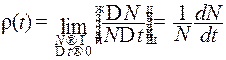 . (2)
. (2)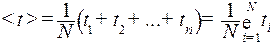 . (3)
. (3)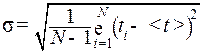 . (4)
. (4)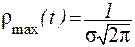 , (5)
, (5)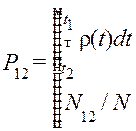 , (6)
, (6)


